Question

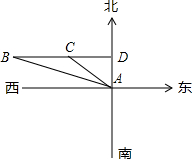
某石油勘探队在荒漠中计划从A地出发，先沿北偏西60°方向勘探4.3km至C地，然后沿正西方向勘探5km至B地，再由B沿直线回到A地．
（1）以1：100 000的比例尺画出勘探与返回的路线图；
（2）勘探队从B地返回到A地应按什么方向？路程是多少千米？

Answer 1

分析：根据方位角的概念，画图正确表示出方位角，再结合三角形的内角和与外角的关系以及勾股定理求解．

解答：解：从A点向北偏东60度方向，按比例尺画出AC=4.3千米，再从A点向正北方向画一条直线AD=4.3/2=2.15千米，连接CD，并延长DC至B，使CB=5千米（如果有60度的直角三角板，则用三角板画），则在△ABC中，AD垂直BC，∠CAD=60°，∠ACD=30°，AD=4.3÷2=2.15，根据勾股定理即可求出CD的=

4.32-2.152

=

13.8675

（千米），
再在直角三角形ABD中，已知BC=5千米，
则BD=BC+CD=（5+

13.8675

）千米，再根据勾股定理可求得AB=

AD2+BD2

=8.985千米，
还可求出角ABC=37.03°．
即AB的长度是返回路程，∠ABC的余角是沿南偏东方向返回的角度．
∴B按南偏东52.57度返回，路程是8.985千米．

点评：解答此类题需要从运动的角度，正确画出方位角，再结合三角形的内角和与外角的关系以及勾股定理求解．