
【题目】为预防禽流感,上海建立了候鸟监测站,某候鸟监测站将一天7点至17点监测到上空飞过的候鸟数制成了如下直方图:
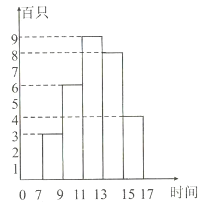
(1)候鸟飞过的高峰期在一天的______;
(2)这一天7点至17点期间,平均每小时飞过上空的候鸟有______只;
(3)每两个小时飞过上空的候鸟数的中位数是______;
(4)若一天飞过上空的候鸟数按此估算,该监测站九月份监测到的候乌只数约是______只;
(5)7时—9时段的频率是______.
【答案】(1)11点~13点;(2)300;(3)6百只;(4)216000;(5)0.1
【解析】
(1)根据直方图可直接得出结果;
(2)从图得到各时间段飞过上空的的候鸟数,再由平均数公式计算每小时飞过上空的候鸟数;
(3)每小时飞过上空的候鸟数从小到大排列,可得中位数;
(4)根据每天飞过上空的候鸟数×小时数×九月份的天数计算即可;
(5)由频率=频数÷数据总数计算7时—9时段候鸟出现的频率.
解:(1)根据直方图可得:候鸟飞过的高峰期在一天的11点~13点;
(2)平均每小时飞过上空的候鸟有![]() =300(只);
=300(只);
(3)小时飞过上空的候鸟数从小到大排列为:3,4,6,8,9(单位:百只),
故每两个小时飞过上空的候鸟数的中位数是6百只;
(4)300×24×30=216000(只),
该监测站九月份监测到的候乌只数约是216000只;
(5)7时—9时段的频率是![]() =0.1.
=0.1.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】一辆从A站开往D站的动车,途中经停B、C两站,互不相识的甲、乙、丙三人同时从A站上车。
(1)求甲、乙两人在同一车站下车的概率;
(2)甲、乙、丙三人在同一车站下车的概率为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C为坐标原点,点![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转90°.
绕点A顺时针旋转90°.
(1)在图中画出旋转后的![]() ,并写出点
,并写出点![]() 、
、![]() 的坐标;
的坐标;
(2)已知点![]() ,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出
,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出![]() 的最小值;
的最小值;
(3)写出![]() 在旋转过程中,线段AB扫过的面积
在旋转过程中,线段AB扫过的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE

(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形![]() 中,
中,![]() 是对角线,点
是对角线,点![]() 为矩形外一点且满足
为矩形外一点且满足![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)若![]() ,
,![]() ,求矩形
,求矩形![]() 的面积;
的面积;
(2)若![]() ,试判断线段
,试判断线段![]() 、
、![]() 、
、![]() 之间的关系,并证明.
之间的关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(-1,0),B(5,0),C(0,-![]() )三点.
)三点.
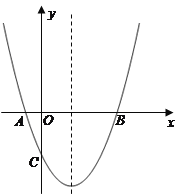
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地都相同的乒乓球,球面上分别标有数字1,2,3,4,小明先从布袋中随机摸出一个乒乓球,不放回去,再从剩下的3个球中随机摸出第二个乒乓球.
(1)求小明第一次摸出的乒乓球所标数字是偶数的概率;
(2)请用树状图或列表的方法求两次摸出的乒乓球球面上数字的积为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com