
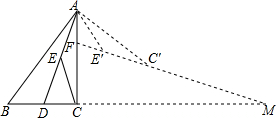
 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$. 分析 分一下几步计算:(1)作辅助线构建直角三角形;(2)证明△CAB≌△CAB′得CB′=CB,∠ABC═∠AB′C;
(3)利用两角对应相等证明△CHB∽△CBA,得①式和②式;(4)利用两角对应相等证明△HAB∽△B′E′M,得出③式;
(5)根据已知BC=3,AC=4和勾股定理求出AB=5及B′C=3,代入①②求出BH、CH、AH的长;
(6)证明Rt△ADK≌Rt△ADC得BK=1,证明Rt△KBD∽Rt△CBA得CD=$\frac{4}{3}$,利用勾股定理求AD的长,利用中点求出AE的长,利用旋转的性质求出AE′的长,得出B′E′的长;(7)代入③式求B′M的长,则CM=B′C+B′M.
解答 解:延长AE′交BM于B′,过B作BG⊥AB′,垂足为G,交AC于H,过D作DK⊥AB,垂足为K,
在Rt△ACD中,E是AD中点,则CE=$\frac{1}{2}AD$=AE=DE,
由旋转得:C′E′=CE,AE′=AE,∠E′AC′=∠EAC,AC′=AC,
∴C′E′=CE′=AE′=AE,∠E′AC′=∠E′C′A=∠EAC,
∵∠AE′F=∠E′AC′+∠E′C′A=2∠EAC,
已知AF=E′F,所以△AFE′是等腰三角形,即∠FAE′=∠FE′A,
∴∠CAB′=2∠EAC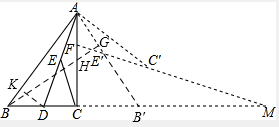 ,
,
已知AD平分∠CAB,
∴∠CAB=2∠DAC,
∴∠CAB′=2∠EAC=∠CAB,
∴△CAB≌△CAB′,
⇒CB′=CB,∠ABC═∠AB′C,
∵BG⊥AB′,
∴∠B′BG=∠B′AC=∠BAC⇒△CHB∽△CBA,
∴$\frac{BH}{AB}=\frac{BC}{AC}$⇒BH=AB•$\frac{BC}{AC}①$,
$\frac{CH}{BC}=\frac{BC}{AC}$⇒CH=BC•$\frac{BC}{AC}②$,
∵∠ABH=∠ABC-∠BAC,
又∵∠AB′B=′B′E′M+∠M⇒∠M=∠ABC-∠CAB′=∠ABC-∠BAC,
∴∠M=∠ABH,
又∠B′E′M=′FE′A=∠FAE′=∠B′AC=∠BAC,
∴△HAB∽△B′E′M⇒$\frac{B′M}{B′E′}=\frac{BH}{AH}$,
⇒B′M=B′E′•$\frac{BH}{AH}③$,
已知BC=3,AC=4,所以AB=5,
∴B′C=BC=3,
代入①式得:BH=5×$\frac{3}{4}$=$\frac{15}{4}$,
代入②式得;CH=3×$\frac{3}{4}$=$\frac{9}{4}$⇒AH=AC-CH=$\frac{7}{4}$,
∵DK⊥AB,又AD平分∠CAB,
得Rt△ADK≌Rt△ADC,
∴AK=AC=4,DC=DK⇒BK=AB-AK=5-4=1,
则Rt△KBD∽Rt△CBA,
∴$\frac{DK}{AC}=\frac{BK}{BC}$⇒CD=DK=AC•$\frac{BK}{BC}$=$\frac{4}{3}$,
⇒AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+(\frac{4}{3})^{2}}$=$\frac{4}{3}\sqrt{10}$,
∵E是AD的中点,
∴EA=$\frac{1}{2}$AD=$\frac{2}{3}\sqrt{10}$,
∴E′A=EA=$\frac{2}{3}\sqrt{10}$⇒B′E′=AB′-E′A=AB-EA=5-$\frac{2}{3}\sqrt{10}$,
根据③式得:B′M=B′E′•$\frac{BH}{AH}$=(5-$\frac{2}{3}\sqrt{10}$)•$\frac{\frac{15}{4}}{\frac{7}{4}}$=$\frac{5}{7}(15-2\sqrt{10})$,
∴CM=B′C+B′M=3+$\frac{5}{7}(15-2\sqrt{10})$=$\frac{96-10\sqrt{10}}{7}$;
故答案为:$\frac{96-10\sqrt{10}}{7}$.
点评 本题考查了旋转的性质,综合性较强;运用了旋转的性质:旋转前后的对应边和对应角相等,等腰三角形中等边对等角,同时综合运用了全等三角形和相似三角形的性质和判定来求边的长,作辅助线把所求的边分成两部分求,利用等量代换求出所得结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
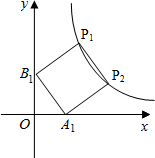 如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com