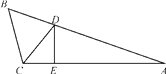
【题目】如图，在△ABC中，∠A＝20°，CD是∠BCA的平分线，△CDA中，DE是CA边上的高，又有∠EDA＝∠CDB，求∠B的大小．
【答案】∠B＝60°.
【解析】试题分析：∠A＝20°，DE是CA边上的高，所以∠EDA＝∠CDB=90°-20°=70°，根据外角的性质得∠CDB=∠A+∠DCE=70°，所以∠DCE=∠BCD=50°，所以∠B=180°-∠BCD-∠CDB=60°.
∵DE是CA边上的高，
∴∠DEA＝∠DEC＝90°.
∵∠A＝20°，
∴∠EDA＝90°－20°＝70°.
∵∠EDA＝∠CDB，
∴∠CDE＝180°－70°×2＝40°.
在Rt△CDE中，∠DCE＝90°－40°＝50°.
∵CD是∠BCA的平分线，
∴∠BCA＝2∠DCE＝2×50°＝100°.
∴∠B＝180°－∠BCA－∠A＝60°.
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E是AD上一点，F是BA延长线上的一点，AF=AE，．
（1）求证：△ABE≌△ADF
（2）线段BE与DF有什么关系？证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知整数a0，a1，a2，a3，a4，…，满足下列条件：a0＝0，a1＝﹣|a0+1|，a2＝﹣|a1+2|，a3＝﹣|a2+3|，…，以此类推，a2019的值是（ ）
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC外，若∠2＝18°，则∠1的度数为（ ）
A. 50°B. 98°C. 75°D. 80°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】嘉淇准备完成题目：化简：
，发现系数“
”印刷不清楚．
（1）他把“”猜成3，请你化简：（3x2+6x+8）–（6x+5x2+2）；
（2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，∠A=∠C=90°，BE，DF分别是∠ABC，∠ADC的平分线．
（1）∠1与∠2有什么关系，为什么？
（2）BE与DF有什么关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】体育文化用品商店购进篮球和排球共20个，进价和售价如下表，全部销售完后共获利润260元．
篮球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 95 | 60 |
求：（1）购进篮球和排球各多少个？
（2）销售6个排球的利润与销售几个篮球的利润相等？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在△ABC中,∠A=640,∠ABC和∠ACD的平分线交于点A1,得∠A1；∠A1BC和∠A1CD的平分线交于点A2,得∠A2；∠A2BC和∠A2CD的平分线交于点A3,则∠A5= ______ ．
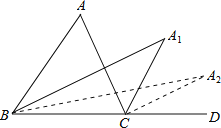
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
