
分析 首先假设成立,根据菱形的性质求解,求得m=±$\sqrt{3}$.
解答 解:假设抛物线C1上存在点P,使得四边形ABCP为菱形,
则PC=AB=BC,
过点A作抛物线C1的对称轴,交x轴于D,过点C作CE⊥AD于E,如图所示:
∵点A与点B关于y轴对称,点C又在y轴上,
∴AC=BC.
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠ACM=∠BCM=30°,
∵四边形ABCP为菱形,且点P在C1上,
∴点P与点C关于AD对称.
∴PC与AD的交点也为点E,
因此∠ACE=90°-30°=60°.
∵点A,C的坐标分别为A(m,m2+1),C(0,1),
∴AE=m2+1-1=m2,CE=|m|,
在Rt△ACE中,tan60°=$\frac{AE}{CE}$=$\sqrt{3}$.
∴m=±$\sqrt{3}$,
故答案为:±$\sqrt{3}$.
点评 此题考查了二次函数与四边形以及轴对称图形的综合知识;解题时要注意辅助线选择与应用,还要注意数形结合思想的应用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
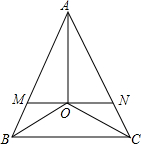 (1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?
(1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$×$\sqrt{11}$ | B. | $\sqrt{10}$×$\sqrt{12}$ | C. | $\sqrt{11}$×$\sqrt{13}$ | D. | $\sqrt{12}$×$\sqrt{14}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com