
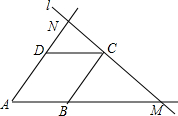
 如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则$\frac{1}{AM}$+$\frac{1}{AN}$=1.
如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则$\frac{1}{AM}$+$\frac{1}{AN}$=1. 分析 根据四边形ABCD是菱形得到BC∥AD,从而得到$\frac{AB}{AM}$=$\frac{NC}{MN}$,根据CD∥AM得到$\frac{AD}{AN}=\frac{MC}{MN}$,从而得到$\frac{AD}{AN}+\frac{AB}{AM}$=$\frac{NC}{MN}+\frac{MC}{MN}$=1,代入菱形的边长为1即可求得结论.
解答 证明:∵四边形ABCD是菱形,
∴BC∥AD,CD∥AM,
∴$\frac{AB}{AM}$=$\frac{NC}{MN}$,$\frac{AD}{AN}=\frac{MC}{MN}$,
∴$\frac{AD}{AN}+\frac{AB}{AM}$=$\frac{NC}{MN}+\frac{MC}{MN}$=1,
又∵AB=AD=1,
∴$\frac{1}{AM}$+$\frac{1}{AN}$=1.
故答案为:1.
点评 本题主要考查了相似三角形的判定与性质、菱形的判定及平行线分线段成比例定理,根据这个定理可以把线段的比进行转化.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
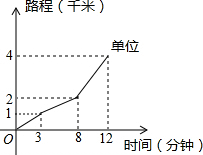 小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )
小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
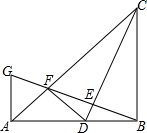 如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )
如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等且相互垂直的四边形是菱形 | |
| B. | 四条边相等的四边形是正方形 | |
| C. | 对角线相互垂直的四边形是平行四边形 | |
| D. | 对角线相等且相互平分的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25 | B. | 0.4 | C. | 0.45 | D. | 0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com