
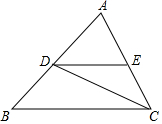
 已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件
已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件分析 (1)根据题意写出命题即可;
(2)根据题意写出已知,求证,证明命题即可.
解答 解:(1)在△ABC中,2∠B=∠ACB,给出下列3个条件,
①如果CD平分∠ACB,DE平分∠ADE,那么DE∥BC;是真命题;
②如果DE平分∠ADE,DE∥BC,那么CD平分∠ACB;真命题;
③如果DE平分∠ADE,DE∥BC,那么CD平分∠ACB;真命题;
∴真命题的个数是3个,
故答案为:3;(2)已知:在△ABC中,2∠B=∠ACB,CD平分∠ACB,DE平分∠ADE,
求证:DE∥BC,
证明:①∵2∠B=∠ACB,∠ACD=∠BCD,
∴∠ACD=∠BCD=∠B,
∴∠ADC=2∠BCD,
∵∠ADE=∠EDC,
∴∠EDC=∠BCD,
∴DE∥BC.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.掌握平行线的性质和角平分线的定义是解题的关键.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
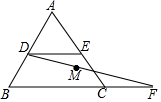 如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.
如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
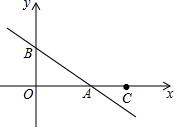 如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).
如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2.
已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 11 | C. | 23 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com