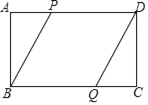
【题目】如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ．
（1）求证：BP=DQ；
（2）若AB=4，且当PD=5时四边形PBQD为菱形．求AD为多少．
【答案】（1）见解析；（2）8.
【解析】
（1）依据矩形的性质，通过全等三角形的判定定理判定△ABP≌△QCD，所以BP=DQ．
（2）设AP=a，AD=5+a．当四边形PBQD是菱形时，PB=PD=5．在直角△ABP中，根据勾股定理得到AP2+AB2=PB2，即a2+42=52，由此可以求得a，再可得AD的长度．
证明：（1）∵四边形ABCD是矩形，
∴∠A=∠C=90°，AB=CD，
在Rt△ABP和Rt△QCD中，
∴△ABP≌△QCD（ASA），
∴BP=DQ；
（2）设AP=a，AD=5+a．
当四边形PBQD是菱形时，PB=PD=5，
在直角△ABP中，根据勾股定理得到AP2+AB2=PB2，即a2+42=52，
可得：a=3，
所以AD=3+5=8．
冲刺100分1号卷系列答案
期末好成绩系列答案科目：初中数学 来源： 题型：
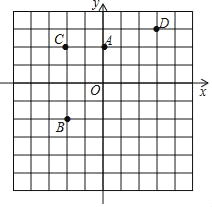
【题目】如图，平面直角坐标系中有4个点：A（0，2），B（﹣2，﹣2），C（﹣2，2），D（3，3）．
（1）在正方形网格中画出△ABC的外接圆⊙M，圆心M的坐标是 ；
（2）若EF是⊙M的一条长为4的弦，点G为弦EF的中点，求DG的最大值；
（3）点P在直线MB上，若⊙M上存在一点Q，使得P、Q两点间距离小于1，直接写出点P横坐标的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一块面积为100cm2的正方形纸片．
（1）该正方形纸片的边长为 cm（直接写出结果）；
（2）小丽想沿着该纸片边的方向裁剪出一块面积为90cm2的长方形纸片，使它的长宽之比为4：3．小丽能用这块纸片裁剪出符合要求的纸片吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
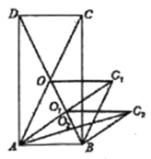
【题目】如图，矩形
的面积为28，对角线交于点
；以
、
为邻边作平行四边形
，对角线交于点
；以、
为邻边作平行四边形
；…依此类推，则平行四边形
的面积为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，我们把横 、纵坐标都是整数的点叫做整点．已知点
A（0，4），点B是
轴正半轴上的整点，记△AOB内部（不包括边界）的整点个数为m．当m=3时，点B的横坐标的所有可能值是 ▲ ；当点B的横坐标为4n（n为正整数）时，m= （用含n的代数式表示．）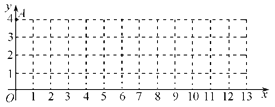
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将几个小正方形与小长方形拼成一个边长为（a+b+c）的正方形．
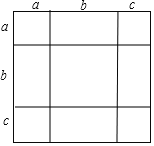
（1）若用不同的方法计算这个边长为（a+b+c）的正方形面积，就可以得到一个的等式，这个等式可以为 ；
（2）请利用（1）中的等式解答下列问题：
①若三个实数a，b，c满足a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值；
②若三个实数x，y，z满足2x×4y÷8z＝32，x2+4y2+9z2＝45，求2xy﹣3xz﹣6yz的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读并回答问题．
求一元二次方程ax2+bx+c=0（a≠0）的根（用配方法）．
解：ax2+bx+c=0，
∵a≠0，∴x2+
x+
=0，第一步
移项得：x2+x=﹣，第二步
两边同时加上（
）2，得x2+x+（____）2=﹣+（）2，第三步
整理得：（x+）2=
直接开方得x+=±
，第四步
∴x=
，
∴x1=
，x2=
，第五步
上述解题过程是否有错误？若有，说明在第几步，指明产生错误的原因，写出正确的过程；若没有，请说明上述解题过程所用的方法．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com