
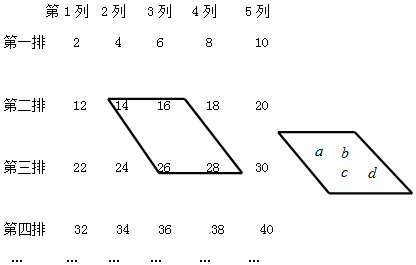
分析 (1)结合数阵,分别用b表示出a、c、d,由此即可得出结论;
(2)假设能求出来.结合(1)可得出a+b+c+d=4b+20,令其等于172,可得出关于b的一元一次方程,解方程求出b值,再找出a、c、d的值,看其是否满足数阵的排列,由此即可得出结论.
(3)由2016的个位不为0可知其不在第5列,根据数阵排和列(第5列除外)中数的特点,即可得出结论;
(4)假设可以,结合(2)可得出关于b的一元一次方程,解方程求出b值,再找出a、c、d的值,根据c、d值结合数阵特点可知其不在同一行,故假设不成立,进而得出结论.
解答 解:(1)由数阵可知:a=b-2,c=b+10,d=c+2=b+12,
∴a+d=b+(b+10)=b+c.
故答案为:a+d=b+c.
(2)假设能求出来.
由(1)可知:a+b+c+d=4b+20=172,
解得:b=38,
∴a=36,c=48,d=50,
∴d=50个位为0,符合数阵的排列.
∴假设成立.
故能求出这四个数,这四个数分别为36、38、48、50.
(3)∵2016个位不为0,
∴2016肯定不在第5列.
∵第一排十位为1,第二排十位为2,第三排十位为3,第四排十位为4,…(第5列除外),2016有201个十和6个一组成,
∴2016在第201排,
∵第1列个位为2,第2列个位为4,第3列个位为6,第4列个位为8,
∴2016在第3列.
故答案为:201;3.
(4)假设可以,
由(2)可知:4b+20=2020,
解得:b=500,
∴c=510,d=512,
c、d不在同一行,
故假设不成立,四个数的和不能是2020.
点评 本题考查了一元一次方程的应用,根据数阵数的分布的特点列出方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
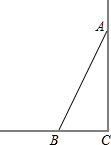 如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )
如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )| A. | 2m | B. | 3m | C. | 4m | D. | $\sqrt{34}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com