
【题目】如图,已知点A是反比例函数![]() 的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为________.
的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为________.

【答案】![]()
【解析】
设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,易证△ACO≌△ODB,即可求得AC=OD=n,CO=BD=-m,由此可得点B的坐标,从而求得点B所在图象的函数表达式.
∵点A是反比例函数![]() 的图象上的一个动点,
的图象上的一个动点,
设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,

∴AC=n,OC=-m,
∴∠ACO=∠ADO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中, ,
,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=-m,
∴B(n,-m),
∵mn=-2,
∴n(-m)=2,
∴点B所在图象的函数表达式为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
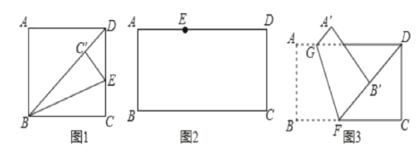
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=46°,则∠DBE的度数为______.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG=![]() ,求B'D的长;
,求B'D的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
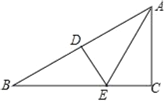
【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=a,BC=2a,点P在边BA上,点Q在边CD上,且BP=m,CQ=n,其中,m<a,n<a,m≠n,在长方形ABCD中,分别以BP、CQ为边作正方形BPP1P2,正方形CQQ1Q2(点P2、Q2在边BC上).
(1)画出图形.

(2)当m<n时,求三角形PQ1C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
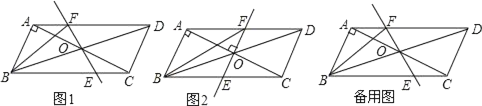
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=![]() ,且BF=DF,求旋转角度α的大小.
,且BF=DF,求旋转角度α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
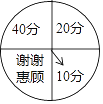
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式![]() 中,
中,![]() 表示这个多项式的项数,
表示这个多项式的项数,![]() 表示这个多项式中三次项的系数.在数轴上点
表示这个多项式中三次项的系数.在数轴上点![]() 与点
与点![]() 所表示的数恰好可以用
所表示的数恰好可以用![]() 与
与![]() 分别表示.有一个动点
分别表示.有一个动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)![]() ________,
________,![]() ___________,线段
___________,线段![]() _________个单位长度;
_________个单位长度;
(2)点![]() 所表示数是________(用含
所表示数是________(用含![]() 的多项式表示);
的多项式表示);
(3)求当![]() 为多少时,线段
为多少时,线段![]() 的长度恰好是线段
的长度恰好是线段![]() 长度的三倍?
长度的三倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
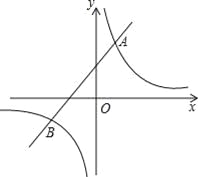
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com