
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 |
|
|
|
|
面试 |
|
|
|
|
(1)这![]() 名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
名选手笔试成绩的中位数是____________分,面试的众数是_____________分;
(2)该公司规定:笔试、面试分别按![]() ,
,![]() 的比例计总分,请比较甲、乙的总分的大小.
的比例计总分,请比较甲、乙的总分的大小.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
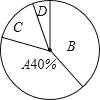
【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,分别将![]() 、
、![]() 沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
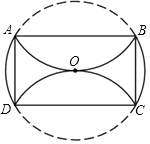
A.8B.![]() C.32D.
C.32D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
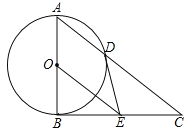
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若千间标准客房,当房价为200元/间时,日均入住数为60间.市场调查表明,在物价局核定的每间标准房价格在160~220元之间(含160元,220元)浮动时,每提高10元,日均入住数减少10间.在不考虑其他因素的前提下,设标准房的价格为x元/间,日均入住数为y间. .
(1) y关于x的解析式为_ .
(2)当标准房的价格定为多少元时,客房的日营业额为10500元?
(3)当标准房的价格定为多少元时,客房的日营业额最大,最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
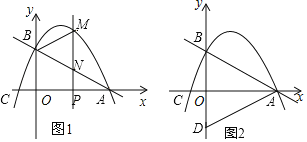
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0)和点C,与y轴交于点B.
(1)求抛物线解析式和点B坐标;
(2)在x轴上有一动点P(m,0)过点P作x轴的垂线交直线AB于点N,交抛物线与点M,当点M位于第一象限图象上,连接AM,BM,求△ABM面积的最大值及此时M点的坐标;
(3)如图2,点B关于x轴的对称点为D,连接AD,BC.
①填空:点P是线段AC上一点(不与点A、C重合),点Q是线段AB上一点(不与点A、B重合),则两条线段之和PQ+BP的最小值为 ;
②填空:将△ABC绕点A逆时针旋转a(0°<α<180°),当点C的对应点C′落在△ABD的边所在直线上时,则此时点B的对应点B′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的表达式是![]() ,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=
,它与两坐标轴分别交于C、D两点,且∠OCD=60,设点A的坐标为(m,0),若以A为圆心,2为半径的⊙A与直线l相交于M、N两点,当MN=![]() 时,m的值为( )
时,m的值为( )
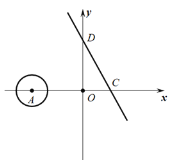
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某校举行冬季运动会,其中一个项目是乒乓球比赛,比赛为单循环制,即所有参赛选手彼此恰好比赛一场. 记分规则是:每场比赛胜者得3分、负者得0分、平局各得1分. 赛后统计,所有参赛者的得分总知为210分,且平局数不超过比赛总场数的![]() ,本次友谊赛共有参赛选手__________人.
,本次友谊赛共有参赛选手__________人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com