
在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a,b,c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根,求△ABC的周长.
m=0的两个实数根,求△ABC的周长.
|
解答:∵b和c是方程x2+mx+2- 当a为一腰长时,则有b=a或c=a. ∴方程必有一根为3,把x=3代入方程,解得m=- ∵b+c= ∴a+b+c=3+ 当a为一底边长时,则b=c,所以原方程有两个相等实数根. ∴Δ=m2-4(2- ∵b+c=-m>0,∴m<0,∴m=2(舍去), 当m=-4时,b+c=4>a,bc=4>0,∴m=-4符合题意. ∴a+b+c=3+4=7. ∴△ABC的周长为 |
|
名师导引:a为腰长时,方程有一根为3,利用方程解的意义和根与系数关系求出b和c,a为底边长时,b和c为三角形腰长,则b=c,所以一元二次方程根的判别式为零,求出b和c. |


科目:初中数学 来源: 题型:
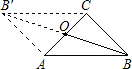 在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距
在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com