
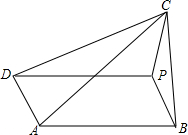
 四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.
四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然. 分析 以PD,PC为一组邻边作平行四边形PCED,连接AE,得到四边形ABCE是平行四边形,证得求出AE=BC,证得△ADE≌△BPC,求得∠DAE=∠CBP,∠AED=∠BCP,当∠CBP=∠CDP时,推出A,D,E,C四点共圆,得到∠ACD=∠AED=∠BCP,当∠ACD=∠BCP时,∠ACD=∠BCP=∠AED,推出A,D,E,C四点共圆,得到∠DAE=∠DCE,由于PD∥CE,得到∠DCE=∠CDP,于是得到结论.
解答 证明: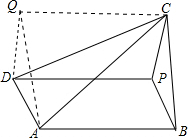 以PD,PC为一组邻边作平行四边形PCED,
以PD,PC为一组邻边作平行四边形PCED,
连接AE,
∴CE∥PD,CE=PD,
∵PD∥AB,PD=AB,
∴CE∥AB,CE=AB,
∴四边形ABCE是平行四边形,
∴AE=BC,
在△ADE与△BPC中,
$\left\{\begin{array}{l}{AE=BC}\\{DE=PC}\\{AD=BP}\end{array}\right.$,
∴△ADE≌△BPC(SSS),
∴∠DAE=∠CBP,∠AED=∠BCP,
当∠CBP=∠CDP时,
∵PD∥CE,
∴∠DCE=∠CDP=∠CBP=∠DAE,
∴A,D,E,C四点共圆,∴∠ACD=∠AED=∠BCP,
当∠ACD=∠BCP时,∠ACD=∠BCP=∠AED,
∴A,D,E,C四点共圆,
∴∠DAE=∠DCE,
∵PD∥CE,
∴∠DCE=∠CDP,
∴∠CDP=∠DAE=∠CBP.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定与性质,四点共圆,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
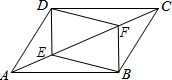 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.
老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
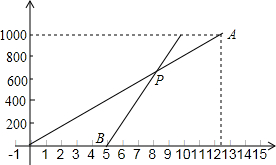 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com