
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
(1)以图中的点O为位似中心,将△ABC作位似变换且同向放大到原来的两倍,得到△A1B1C1;
(2)若△ABC内一点P的坐标为(a,b),则位似变化后对应的点P′的坐标是 . 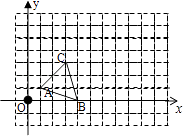
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为( )
A.2cm
B.14cm
C.2cm或14cm
D.10cm或20cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°. 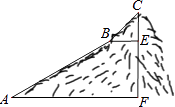
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1 , △2 , △3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( ) 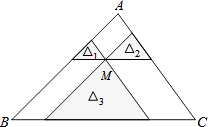
A.49
B.64
C.100
D.81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的剧烈为碟高.
(1)抛物线y=x2对应的碟宽为;抛物线y= ![]() x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
(2)利用图(1)中的结论:抛物线y=ax2﹣4ax﹣ ![]() (a>0)对应的碟宽为6,求抛物线的解析式.
(a>0)对应的碟宽为6,求抛物线的解析式.
(3)将抛物线yn=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3,…),定义F1 , F2 , …..Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ![]() ,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
①求抛物线y2的表达式;
②若F1的碟高为h1 , F2的碟高为h2 , …Fn的碟高为hn . 则hn= , Fn的碟宽右端点横坐标为 . 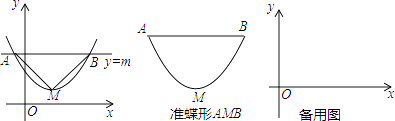
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,﹣2). 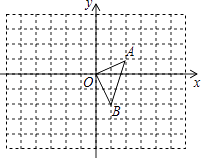
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的位似比为2:1,并分别写出点A,B的对应点A1、B1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2 , 并写出点A,B的对应点A2、B2的坐标;
(3)判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点. 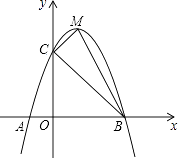
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com