
 我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:阅读理解
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
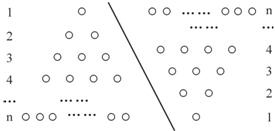
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
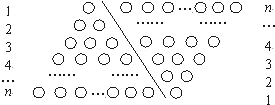 并利用图形做必要的推理说明)
并利用图形做必要的推理说明)查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 210 |
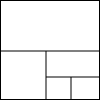 出最后余下未贴部分的面积的表达式:
出最后余下未贴部分的面积的表达式:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com