

���� ��1�������ı���ABCD��$\sqrt{2}$���εĶ��壬ֻҪ֤��AD=$\sqrt{2}$CD���ɣ�
��2����������ABCD�ı߳�Ϊ1�����BF�ij����ɽ�����⣮
��� �⣺��1���ı���ABCD��$\sqrt{2}$���Σ�
���ɣ����ı���ABCD�Ǿ��Σ�
���EDC=��DEF=��C=90�㣬
��DE=DC��
���ı���CDEF�������Σ�
��DF=$\sqrt{2}$DC����AD=DF
��AD=$\sqrt{2}$DC��
�����ABCD��$\sqrt{2}$����
��2����������ABCD�ı߳�Ϊ1����$BD=\sqrt{2}$��
���۵����ʿ�֪BG=BC=1����AFE=��BFE=90�㣬���ı���BCEFΪ���Σ�
���A=��BFE��
��EF��AD��
��$\frac{BG}{BD}=\frac{BF}{AB}$����$\frac{1}{{\sqrt{2}}}=\frac{BF}{1}$��
��BF=$\frac{1}{{\sqrt{2}}}$��
��BC��BF=1��$\frac{1}{{\sqrt{2}}}$=$\sqrt{2}$��1��
���ı���BCEFΪ$\sqrt{2}$���Σ�
���� ���⿼����Ρ������ε����ʡ����ɶ�����֪ʶ������Ĺؼ����������⣬��֤���ı�����$\sqrt{2}$���Σ�ֻҪ֤������ı��εij�����֮��Ϊ$\sqrt{2}$�������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -20% | B�� | 40% | C�� | -220% | D�� | 20% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
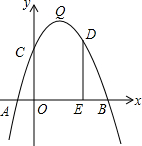 ��ͼ��������y=-x2+bx+c�Ķ���ΪQ����������x�ύ��A��-1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��ͼ��������y=-x2+bx+c�Ķ���ΪQ����������x�ύ��A��-1��0����B��5��0�����㣬��y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�ı�AB=3��AD=4����E�ӵ�A������������AD�ƶ�����CEΪֱ����ԲO����FΪԲO������BD�Ĺ����㣬����EF��CF������E��EG��EF��EG��ԲO�ཻ�ڵ�G������CG��
��ͼ������ABCD�ı�AB=3��AD=4����E�ӵ�A������������AD�ƶ�����CEΪֱ����ԲO����FΪԲO������BD�Ĺ����㣬����EF��CF������E��EG��EF��EG��ԲO�ཻ�ڵ�G������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2•a3=a6 | B�� | ��b2��3=b6 | C�� | ��3m��2=6m2 | D�� | x3��x3=x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com