
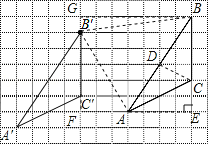
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.

(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是: ;
(4)求四边形ACBB′的面积.
【答案】(1)见解析;(2)见解析;(3)平行且相等;(4)11
【解析】
试题分析:(1)根据图形平移的性质画出△A′B′C′即可;
(2)取线段AB的中点D,连接CD,过点A作AE⊥BC的延长线与点E即可;
(3)根据图形平移的性质可直接得出结论;
(4)根据S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′即可得出结论.
解:(1)如图所示;
(2)如图所示;
(3)由图形平移的性质可知,AA′∥BB′,AA′=BB′.
故答案为:平行且相等;
(4)S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′
=![]() (7+3)×6+
(7+3)×6+![]() ×4×4﹣
×4×4﹣![]() ×1×7﹣
×1×7﹣![]() ×3×5
×3×5
=30﹣8﹣![]() ﹣
﹣![]()
=11.


科目:初中数学 来源: 题型:
【题目】某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元):
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
-27.8 | -70.3 | 200 | 138.1 | -8 | 188 | 458 |
表中星期六的盈亏数被墨水涂污了,请你通过计算说明星期六的盈亏情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:
我们已经学过将一个多项式分解因式的方泫有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法.
如: ![]() ,
, ![]()
分组分解法:
解:原式![]() 解:原式
解:原式![]()
![]()
![]()
![]()
(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.
如: ![]()
解:原式![]()
![]()
![]()
![]()
请你仿照以上方法,探索并解决下列问题:
(l)分解因式: ![]() ;
;
(2)分解因式: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的![]() 少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
(1)报两门课的共有多少人?
(2)调动后,报名第一门课的人数为 人,第二门课人数为 人.
(3)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x的值代入,并求出具体的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时,点N从B出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN存在时,求运动多少秒使△MBN的面积最大,最大面积是多少?
(3)在(2)的条件下,△MBN面积最大时,在BC上方的抛物线上是否存在点P,使△BPC的面积是△MBN面积的9倍?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列正确说法的是____
①同位角相等; ②等角的补角相等; ③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若![]() ,则
,则![]() =( )
=( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com