
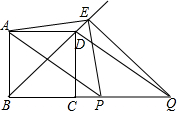
 ��ͼ��BD��������ABCD�ĶԽ��ߣ�BC=2������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ�������BC�˶���ͬʱ����Q�ӵ�C����������ͬ���ٶ�������BC�˶�������P��������Q��QE��BD����ֱ��BD�ڵ�E������AP��AE��PE��QE�����˶�ʱ��Ϊt���룩��
��ͼ��BD��������ABCD�ĶԽ��ߣ�BC=2������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ�������BC�˶���ͬʱ����Q�ӵ�C����������ͬ���ٶ�������BC�˶�������P��������Q��QE��BD����ֱ��BD�ڵ�E������AP��AE��PE��QE�����˶�ʱ��Ϊt���룩������ ��1���������ε����ʺ���֪�����ó���ABE=��EBQ=45�㣬AD��BQ��AD=BC=2��BP=CQ���ó�BC=AD=PQ������֤���ı���APQD��ƽ���ı��Σ�
��2��֤��BE=QE����SAS֤����AEB�ա�EPQ���ó�AE=PE����AEB=��PEQ���ó���AEP=��BEQ=90�㣬���ɵó�AE��PE��
��3����E��EF��BC��F��BQ=t+2��EF=$\frac{t+2}{2}$���ó�y=$\frac{1}{2}$��$\frac{t+2}{2}$��t�����ɵó��𰸣�
��4��������������ٵ�P��BC�ӳ�����ʱ����PM��QE��M���ɵ���ֱ�������ε����ʺ��ɶ����ó�PM=$\frac{\sqrt{2}}{2}$PQ=$\sqrt{2}$��BE=QE=$\frac{\sqrt{2}}{2}$BQ=$\frac{\sqrt{2}}{2}$��t+2�������DE=BE-BD=$\frac{\sqrt{2}}{2}t-\sqrt{2}$���������������ϵ�������ʽ�ó����̣��ⷽ�̼��ɣ�
�ٵ�P��BC����ʱ���ⷨͬ�٣���ʱDE=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t���������������ϵ�������ʽ�ó����̣��ⷽ�̼��ɣ�
��� �⣺��1���ı���APQD��ƽ���ı��Σ��������£�
���ı���ABCD�������Σ�P��Q�ٶ���ͬ��
���ABE=��EBQ=45�㣬AD��BQ��AD=BC=2��BP=CQ��
��BC=AD=PQ��
���ı���APQD��ƽ���ı��Σ�
��2��AE=PE��AE��PE���������£�
��EQ��BD�����PQE=90��-45��=45�㣬
���ABE=��EBQ=��PQE=45�㣬
��BE=QE��
�ڡ�AEB�͡�EPQ�У�$\left\{\begin{array}{l}{AB=PQ}&{\;}\\{��ABE=��PQE}&{\;}\\{BE=QE}&{\;}\end{array}\right.$��
���AEB�ա�EPQ��SAS����
��AE=PE����AEB=��PEQ��
���AEP=��BEQ=90�㣬
��AE��PE��
��3����E��EF��BC��F����ͼ1��ʾ��
BQ=t+2��EF=$\frac{t+2}{2}$��
��y=$\frac{1}{2}$��$\frac{t+2}{2}$��t��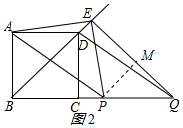
��y=$\frac{1}{4}$t2+$\frac{1}{2}$t��
��4��������������ٵ�P��BC�ӳ�����ʱ����PM��QE��M����ͼ2��ʾ��
��PQ=2����BQE=45�㣬
��PM=$\frac{\sqrt{2}}{2}$PQ=$\sqrt{2}$��BE=QE=$\frac{\sqrt{2}}{2}$BQ=$\frac{\sqrt{2}}{2}$��t+2����
��DE=BE-BD=$\frac{\sqrt{2}}{2}$��t+2��-2$\sqrt{2}$=$\frac{\sqrt{2}}{2}t-\sqrt{2}$��
�ߡ�EPQ��������ǡ�EDQ�����2����
��$\frac{1}{2}$��$\frac{\sqrt{2}}{2}$��t+2����$\sqrt{2}$=2��$\frac{1}{2}$��$\frac{\sqrt{2}}{2}$t-$\sqrt{2}$����$\frac{\sqrt{2}}{2}$��t+2����
��ã�t=3��t=-2����ȥ����
��t=3��
�ٵ�P��BC����ʱ���ⷨͬ�٣���ʱDE=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t��
�ߡ�EPQ��������ǡ�EDQ�����2����
��$\frac{1}{2}$��$\frac{\sqrt{2}}{2}$��t+2����$\sqrt{2}$=2��$\frac{1}{2}$��$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t����$\frac{\sqrt{2}}{2}$��t+2����
��ã�t=1��t=-2����ȥ����
��t=1��
������������EPQ������ǡ�EDQ�����2��ʱt��ֵΪ��1��3��
���� �������ı����ۺ���Ŀ�������������ε����ʡ�ȫ�������ε��ж������ʡ�����ֱ�������ε��ж������ʡ����ɶ����������������ʽ��֪ʶ�������ۺ���ǿ����һ���Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
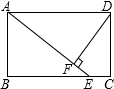 ��֪����ͼ������ABCD�У�E��BC��һ�㣬DF��AE��F����AE=BC�� ��֤��BE=AF��
��֪����ͼ������ABCD�У�E��BC��һ�㣬DF��AE��F����AE=BC�� ��֤��BE=AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
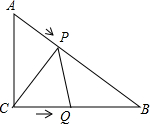 ��֪��Rt��ABC�У���ACB=90�㣬CA=3��CB=4����P��Q�ֱ�ΪAB�ߣ�CB���ϵĶ��㣬����ͬʱ�ֱ��A��C��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����P��Q�˶���ʱ��Ϊt�룮
��֪��Rt��ABC�У���ACB=90�㣬CA=3��CB=4����P��Q�ֱ�ΪAB�ߣ�CB���ϵĶ��㣬����ͬʱ�ֱ��A��C��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����P��Q�˶���ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
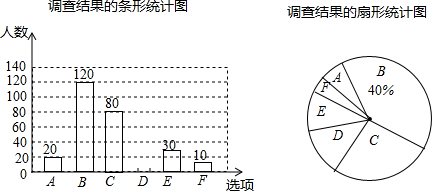
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
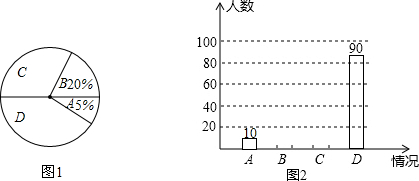
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
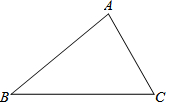 ����������ADE��E���߶�AC�ϣ�D���߶�AB�ϣ�ʹ�á�ADE�ס�ACB��������ͼ�ۼ���
����������ADE��E���߶�AC�ϣ�D���߶�AB�ϣ�ʹ�á�ADE�ס�ACB��������ͼ�ۼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
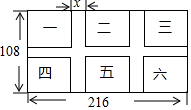 ��ͼ������߲˻�������һ�鳤Ϊ216m����Ϊ108m�ij��������أ���������Ϊxm�����С·�����ֳ������ȵ����飬�ֱ���ֲ���������ƹϡ�������ܿ�����²ˡ����ӣ�
��ͼ������߲˻�������һ�鳤Ϊ216m����Ϊ108m�ij��������أ���������Ϊxm�����С·�����ֳ������ȵ����飬�ֱ���ֲ���������ƹϡ�������ܿ�����²ˡ����ӣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com