练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．数轴上到-$\sqrt{2}$这点距离为$\sqrt{2}$的点表示的数是0或-2$\sqrt{2}$．

    分析 在数轴上表示-$\sqrt{2}$左右两边找出满足题意的数即可．

    解答 解：数轴上到-$\sqrt{2}$这点距离为$\sqrt{2}$的点表示的数是0或-2$\sqrt{2}$，
    故答案为：0或-2$\sqrt{2}$

    点评 此题考查了实数与数轴，解题关键是求数轴上两点间的距离应让较大的数减去较小的数即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

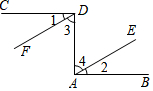    14．如图，已知CD⊥DA，DA⊥AB，∠1=∠2．试说明DF∥AE．请你完成下列填空，把证明过程补充完整．
    证明：∵CD⊥DA，DA⊥AB，，
    ∴∠CDA=90°，∠DAB=90° （垂直定义）．
    ∴∠1+∠3=90°，∠2+∠4=90°．
    又∵∠1=∠2，
    ∴∠3=∠4 （等角的余角相等），
    ∴DF∥AE （内错角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一家游泳馆的游泳收费标准为25元/次，若购买会员年卡，可享受如下优惠：
    会员年卡类型办卡费用（元）每次游泳收费（元）
    A类5020
    B类15015
    C类30010
    例如，购买A类会员卡，一年内游泳20次，消费50+20×20=450元，若一年内在该游泳馆消费500元，则游泳次数最多的办卡方式是（　　）
    A．购买A类会员年卡B．购买B类会员年卡C．购买C类会员年卡D．不购买会员年卡

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

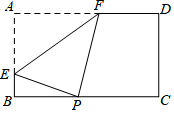    12．如图，矩形纸片ABCD中，AB=6，AD=10，P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别是E，F，要使折痕始终与边AB，AD有交点，则BP的取值范围是（　　）
    A．$\sqrt{5}≤BP≤5$B．2≤BP≤6C．$\sqrt{5}≤BP≤6$D．$2≤BP≤5\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：$\frac{1}{42}$÷（$\frac{1}{6}$-$\frac{2}{7}$+$\frac{2}{3}$-$\frac{3}{14}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．用简便方法计算：20172-2017×4032+20162．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．先阅读下列解题过程，再回答问题：
    计算：$\frac{4}{{x}^{2}-4}$+$\frac{1}{2-x}$
    解：原式=$\frac{4}{（x+2）（x-2）}$-$\frac{1}{x-2}$…①
    =$\frac{4}{（x+2）（x-2）}$-$\frac{x+2}{（x+2）（x-2）}$…②
    =4-（x+2）…③
    =2-x…④
    （1）以上解答有错误，错误步骤的序号是③，错误做法是去分母．
    （2）请你给出正确的解答．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，△ABC是⊙O的内接三角形，连接OB、OC．若∠BOC=120°，则∠BAC的度数为（　　）
    A．30°B．45°C．60°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．化简$\sqrt{{{（1-\sqrt{3}）}^2}}+\sqrt{3}$=2$\sqrt{3}$-1．

    查看答案和解析>>

    同步练习册答案