
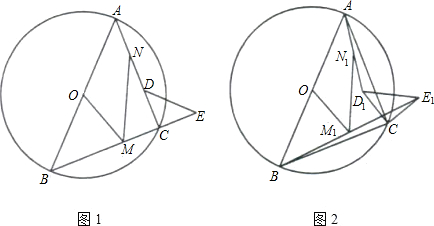
如图7,⊙O中AB是直径,C是⊙O上一点,∠ABC=450,等腰直角三角形DCE中∠DCE是直角,点D在线段AC上。
(1)证明:B、C、E三点共线;
(2)若M是线段BE的中点,N是线段AD的中点,证明:MN=![]() OM;
OM;
(3)将△DCE绕点C逆时针旋转![]() (00<
(00<![]() <900)后,记为△D1CE1(图8),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=
<900)后,记为△D1CE1(图8),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=![]() OM1是否成立?若是,请证明:若不是,说明理由。
OM1是否成立?若是,请证明:若不是,说明理由。


(1)证明:∵ AB是⊙O的直径
∴ ∠ACB=90°
∵ ∠DCE=90°
∴∠ACB+∠DCE=180°
∴ B、C、E三点共线。
(2)证明:连接ON、AE、BD,延长BD交AE于点F
∵ ∠ABC=45°,∠ACB=90°
∴ BC=AC,又∠ACB=∠DCE=90°,DC=EC
∴ △BCD≌△ACE
∴ BD=AE,∠DBC=∠CAE
∴∠DBC+∠AEC=∠CAE+∠AEC=90°
∴ BF⊥AE

∵ AO=OB,AN=ND
∴ ON=![]() BD,ON∥BD
BD,ON∥BD
∵ AO=OB,EM=MB
∴ OM=![]() AE,OM∥AE
AE,OM∥AE
∴ OM=ON,OM⊥ON
∴ ∠OMN=45°,又 cos∠OMN=![]()
∴ ![]()
(3) ![]() 成立,证明同(2)。
成立,证明同(2)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 2 |
| 2 |
 不是,说明理由.
不是,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| m+n | m-n |
 说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案)
说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案)查看答案和解析>>
科目:初中数学 来源: 题型:
| m+n |
| m-n |
 |
| AD |
 |
| BD |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
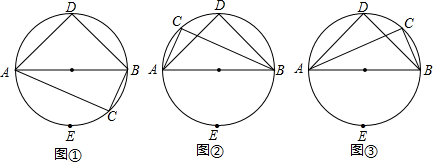
 如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.
如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.| MN |
| OM |
| MN |
| OM |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com