
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{3}$×$\sqrt{5}$=$\sqrt{15}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
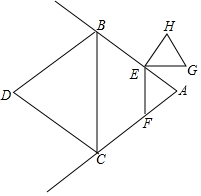 如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.
如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.63×10-6m | B. | 6.3×10-7m | C. | 6.3×10-8m | D. | 63×10-8m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
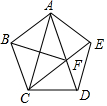 如图,正五边形ABCDE中.连接AC,AD,CE,CE交AD于点F,连接BF.下列说怯正确的是①③④(将所有正确说法的序号填写在横线上).①△ACD的周长大于4CD;②FC平分∠BFD:③四边形ABCF是菱形;④CD2=EF•CE.
如图,正五边形ABCDE中.连接AC,AD,CE,CE交AD于点F,连接BF.下列说怯正确的是①③④(将所有正确说法的序号填写在横线上).①△ACD的周长大于4CD;②FC平分∠BFD:③四边形ABCF是菱形;④CD2=EF•CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com