
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������λ�ڵ�A���һ�㣬��AB=22������P��A���������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1�������ϵ�B��ʾ��������������P��ʾ�������������ú�t�Ĵ���ʽ��ʾ��
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q��
��3����MΪAP���е㣬NΪBP���е㣬�ڵ�P�˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
![]()
���𰸡���1��-14��8-5t����2��11����3�����䡣���ɼ�����.
����������������1��������֪�ɵ�B���ʾ����Ϊ8-22����P��ʾ����Ϊ8-5t����2����P�˶�x��ʱ���ڵ�C���ϵ�Q����AC=5x��BC=3x������AC-BC=AB���г�������⼴�ɣ���3���֢ٵ���P�ڵ�A��B����֮���˶�ʱ���ڵ���P�˶�����B�����ʱ�������е�Ķ�����߶εĺͲ����MN�ij����ɣ�
���������
��1�������ϵ�B��ʾ��������-14������P��ʾ��������8-5t��
��2����P��ʾ�����ǣ�8-5t������Q��ʾ�����ǣ�-14-3t���������⣺
8-5t=-14-3t
�����t=11
���P�˶�11��ʱ�ϵ�Q
��3�����䡣�������£�
��M��AP�������MP=![]() AP
AP
��N��BP�������NP=![]() BP
BP
��MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)= ![]() AB=11
AB=11
�㾦;���⿼���������һԪһ�η��̵�Ӧ�ã��õ���֪ʶ��������������֮��ľ��룬�ؼ��Ǹ������⻭��ͼ�Σ�Ҫ������������ۣ�ע��������۵�˼��.


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�AB��CD��AB=CD���ܳ�Ϊ40cm�����ڱߵı���3��2����ϳ��ߵij����ǣ� ��
A. 8cm B. 10cm C. 12cm D. 14cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м��㲻��ȷ���ǣ�������
A. 30��3��3=9 B. ����4����5=��20 C. ��1��2=��3 D. |����3��+����5��|=8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غϣ�չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF���������н��ۣ��١�ADG=22.5�㣻��tan��AED=2����S��AGD=S��OGD�����ı���AEFG�����Σ���BE=2OG������S��OGF=1����������ABCD�������![]() ��������ȷ�Ľ��۸���Ϊ�� ��
��������ȷ�Ľ��۸���Ϊ�� ��
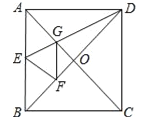
A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����A��B��C����λ��ͼ�Σ���A��B��C�������Ϊ6cm2���ܳ�����ABC��һ�룮AB��8cm����AB���ϸߵ��� �� ��
A. 3 cm B. 6 cm C. 9cm D. 12cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�� 0����1����2���ĸ����У���С�����ǣ� ��
A. ��2 B. ��1 C.0 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC��AC=BC=10��AB=12����BCΪֱ������O��AB�ڵ�D����AC�ڵ�G��DF��AC������ΪF����CB���ӳ����ڵ�E��

��1����֤��ֱ��EF�ǡ�O�����ߣ�
��2����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=6 cm��BC=8 cm���ضԽ���AC�����ηֳ�����ֱ�������Σ����С�ABC��������A��C��D������CA�ķ�����ÿ��2 cm���ٶ��ƶ���
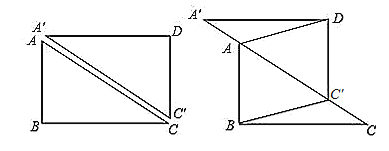
��1����ƽ�ƹ����У��ı���ABC��Dʼ���� ������������ĸ�ѡ����ѡ��һ������Ϊ��ȷ��������ں����ϣ���
��ƽ���ı��� �ھ��� ������ ��������
��2�����ƶ������У����ƶ�ʱ��t���룩Ϊ��ֵʱ���ı���ABC'D�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90�㣬AC=3��BC=4������AC��CD���ۣ�ʹ��A����AB�ϵĵ�E�����ٽ���BC��CF���ۣ�ʹ��B����CE���ӳ����ϵĵ�B�����������ۺ���б��AB�ֱ��ڵ�D��F�����߶�B��F�ij�Ϊ( )
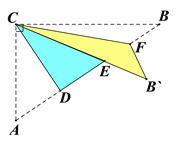
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com