
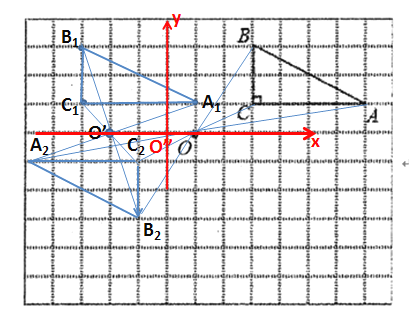
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 都是格点.
都是格点.

(1)将![]() 向左平移6个单位长度得到
向左平移6个单位长度得到![]() ;
;
(2)将![]() 绕点
绕点![]() 按逆时针方向旋转180°得到
按逆时针方向旋转180°得到![]() ,请画出
,请画出![]() ;
;
(3)若点![]() 的坐标为(3,3);写出
的坐标为(3,3);写出![]() 与
与![]() 的对称中心的坐标_____.
的对称中心的坐标_____.
【答案】(1)作图见解析;(2)作图见解析;(3)(-2,0)
【解析】
(1)分别找到A、B、C三点向左平移六个单位后得到的三个点A1、B1、C1,连接A1、B1、C1,即可得到![]() ;
;
(2)将![]() 三个顶点A、B、C绕点
三个顶点A、B、C绕点![]() 按逆时针方向旋转180°得到A2、B2、C2,连接三点A2、B2、C2,即可得到
按逆时针方向旋转180°得到A2、B2、C2,连接三点A2、B2、C2,即可得到![]() ;
;
(3)先找到![]() 与
与![]() 的对称中心点点
的对称中心点点![]() ,根据点
,根据点![]() 的坐标为(3,3),在图中建立直角坐标系即可得出
的坐标为(3,3),在图中建立直角坐标系即可得出![]() 点坐标.
点坐标.
(1)A、B、C三点向左平移六个单位后的点为A1、B1、C1,连接A1、B1、C1,即可得到![]() ,如图所示;
,如图所示;
(2)点A、B、C绕点![]() 按逆时针方向旋转180°后的点为A2、B2、C2,连接三点A2、B2、C2,即可得到
按逆时针方向旋转180°后的点为A2、B2、C2,连接三点A2、B2、C2,即可得到![]() ,如图所示;
,如图所示;
(3)连接A1A2、B1B2、C1C2,得到![]() 与
与![]() 的对称中心点为点
的对称中心点为点![]()
根据点![]() 的坐标为(3,3),
的坐标为(3,3),
可在图中建立直角坐标系![]() ,
,
得出![]() 点坐标为(-2,0)
点坐标为(-2,0)
故答案为:(-2,0)


科目:初中数学 来源: 题型:
【题目】如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°。
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:①参加本次竞赛的学生共有100人;②第五组的百分比为16%;③成绩在70-80分的人数最多;④80分以上的学生有14名;其中正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图像与函数
的图像与函数![]() (
(![]() )的图像相交于点
)的图像相交于点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 与
与![]() 的面积比为3:7.
的面积比为3:7.

(1)![]() _____,
_____,![]() _____.
_____.
(2)求点![]() 的坐标;
的坐标;
(3)若将![]() 绕点
绕点![]() 逆时针旋转,得到
逆时针旋转,得到![]() ,其中点
,其中点![]() 落在
落在![]() 轴负半轴上,判断点
轴负半轴上,判断点![]() 是否落在函数
是否落在函数![]() (
(![]() )的图像上,并说明理由.
)的图像上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC:CB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com