
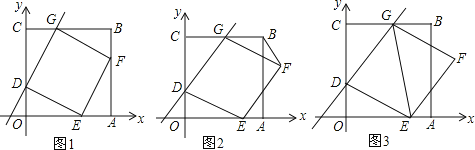
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.
【答案】(1)m=2证明见解析(2)①2;6﹣a(3)m=![]()
【解析】试题分析:(1)将x=0代入y=mx+2得y=2,故此点D的坐标为(0,2),由CG=OD=2可知点G的坐标为(2,6),将点G(2,6)代入y=mx+2可求得m=2;
(2)如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.先证明Rt△GHF≌Rt△EOD,从而得到FH=DO=2,由三角形的面积公式可知:S=6-a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.由菱形的性质可知:DM⊥GM,点M为DF的中点,根据角平分线的性质可知:MD=CD=4,由中点坐标公式可知点M的纵坐标为3,于是得到ND=1,根据勾股定理可求得MN=![]() ,于是得到点M的坐标为(
,于是得到点M的坐标为(![]() ,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=
,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=![]() .
.
解:(1)∵将x=0代入y=mx+2得;y=2,∴点D的坐标为(0,2).
∵CG=OD=2,∴点G的坐标为(2,6).
将点G(2,6)代入y=mx+2得:2m+2=6.解得:m=2.
证明△DOE≌△GCD(HL),再证明∠GDE=90°,即可证出菱形GDEF为正方形.
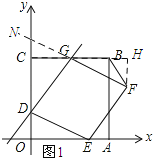
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.
∵四边形DEFG为菱形,∴GF=DE,GF∥DE.∴∠GNC=∠EDO.
∴∠NGC=∠DEO.∴∠HGF=∠DEO.
在Rt△GHF和Rt△EOD中,
 ,
,
∴Rt△GHF≌Rt△EOD.∴FH=DO=2.
∴![]() =
=![]() ×2×(6﹣a)=6﹣a.
×2×(6﹣a)=6﹣a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.
又∵四边形DEFG为菱形,
∴DM⊥GM,点M为DF的中点.
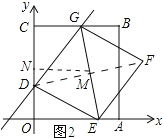 ∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∴MD=CD=4.
∵由(2)可知点F的坐标为4,点D的纵坐标为2,
∴点M的纵坐标为3.
∴ND=1.
在Rt△DNM中,MN=![]() =
=![]() .
.
∴点M的坐标为(![]() ,3).
,3).
设直线DM的解析式为y=kx+2.将(![]() ,3)代入得:
,3)代入得:![]() k+2=3.
k+2=3.
解得:k=![]() .
.
∴设直线MG的解析式为y=![]() x+b.将(
x+b.将(![]() ,3)代入得:﹣15+b=3.
,3)代入得:﹣15+b=3.
解得:b=18.
∴直线MG的解析式为y=﹣![]() x+18.
x+18.
将y=6代入得:![]() .
.
解得:x=![]() .
.
∴点G的坐标为(![]() ,6).
,6).
将(![]() ,6)代入y=mx+2得:
,6)代入y=mx+2得:![]() m+2=6.
m+2=6.
解得:m=![]() .
.


科目:初中数学 来源: 题型:
【题目】背景资料:
在已知△ABC所在平面上求一点P,使它到三角形的三个顶点的距离之和最小.
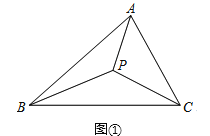
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.
如图①,当△ABC三个内角均小于120°时,费马点P在△ABC内部,此时∠APB=∠BPC=∠CPA=120°,此时,PA+PB+PC的值最小.
解决问题:
(1)如图②,等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA,PB,PC转化到一个三角形中,从而求出∠APB= ;
基本运用:
(2)请你利用第(1)题的解答思想方法,解答下面问题:
如图③,△ABC中,∠CAB=90°,AB=AC,E,F为BC上的点,且∠EAF=45°,判断BE,EF,FC之间的数量关系并证明;
能力提升:
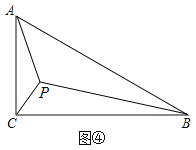
(3)如图④,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点P为Rt△ABC的费马点,
连接AP,BP,CP,求PA+PB+PC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列现象
(1)水平运输带上砖块的运动
(2)高楼电梯上上下下迎接乘客
(3)健身做呼啦圈运动
(4)火车飞驰在一段平直的铁轨上
(5)沸水中气泡的运动
属于平移的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
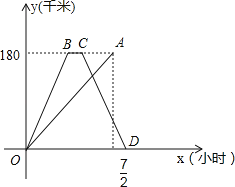
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校给“希望小学”邮寄每册a元的图书240册,若每册图书的邮费为书价的5%,则共需邮费()
A.5%a元B.240a(1+5%)元
C.5%×240a元D.240元
查看答案和解析>>
科目:初中数学 来源: 题型:
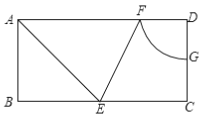
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
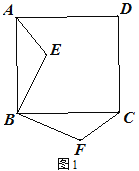
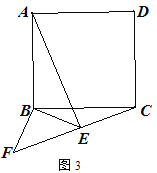
【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①![]() ;②
;②![]() .
.
(2)若![]() ,
,
① 如图2,点E在正方形内,连接EC,若![]() ,
, ![]() ,求
,求![]() 的长;
的长;
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于( )
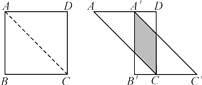
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com