
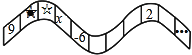
”¾ĢāÄæ”æČēĶ¼£¬“Ó×ó±ßµŚŅ»øöøń×ÓæŖŹ¼ĻņÓŅŹż£¬ŌŚĆæøöŠ”øń×ÓÖŠ¶¼ĢīČėŅ»øöÕūŹż£¬Ź¹µĆĘäÖŠČĪŅāČżøöĻąĮŚøń×ÓÖŠĖłĢīÕūŹżÖ®ŗĶ¶¼ĻąµČ£®
£Ø![]() £©æÉĒóµĆ
£©æÉĒóµĆ![]() __________£¬µŚ
__________£¬µŚ![]() øöøń×ÓÖŠµÄŹżĪŖ__________£®
øöøń×ÓÖŠµÄŹżĪŖ__________£®
£Ø![]() £©ÅŠ¶Ļ£ŗĒ°
£©ÅŠ¶Ļ£ŗĒ°![]() øöøń×ÓÖŠĖłĢīÕūŹżÖ®ŗĶŹĒ·ńæÉÄÜĪŖ
øöøń×ÓÖŠĖłĢīÕūŹżÖ®ŗĶŹĒ·ńæÉÄÜĪŖ![]() £æČōÄÜ£¬Ēó³ö
£æČōÄÜ£¬Ēó³ö![]() µÄÖµ£¬Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ£¬Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø![]() £©ČōČ”Ē°
£©ČōČ”Ē°![]() øń×ÓÖŠµÄČĪŅāĮ½øöŹż¼Ē×÷
øń×ÓÖŠµÄČĪŅāĮ½øöŹż¼Ē×÷![]() ”¢
”¢![]() £¬ĒŅ
£¬ĒŅ![]() £¬ÄĒĆ“ĖłÓŠµÄ
£¬ÄĒĆ“ĖłÓŠµÄ![]() µÄŗĶæÉŅŌĶعż¼ĘĖć
µÄŗĶæÉŅŌĶعż¼ĘĖć![]() µĆµ½£¬Ęä½į¹ūĪŖ__________£»Čō
µĆµ½£¬Ęä½į¹ūĪŖ__________£»Čō![]() ”¢
”¢![]() ĪŖĒ°
ĪŖĒ°![]() øń×ÓÖŠµÄČĪŅāĮ½øöŹż¼Ē×÷
øń×ÓÖŠµÄČĪŅāĮ½øöŹż¼Ē×÷![]() ”¢
”¢![]() £¬ĒŅ
£¬ĒŅ![]() £¬ŌņĖłÓŠµÄ
£¬ŌņĖłÓŠµÄ![]() µÄŗĶĪŖ__________£®
µÄŗĶĪŖ__________£®
”¾“š°ø”æ£Ø![]() £©
£©![]() £»
£» ![]() £Ø
£Ø![]() £©ÄÜ£¬
£©ÄÜ£¬ ![]() £Ø
£Ø![]() £©
£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻČżøöĻąĮŚøń×ÓµÄÕūŹżµÄŗĶĻąµČĮŠŹ½Ēó³öxµÄÖµ£¬ŌŁøł¾ŻµŚ9øöŹżŹĒ2æɵƔī=2£¬Č»ŗóÕŅ³öøń×ÓÖŠµÄŹżŹĒĆæ3øöĪŖŅ»øöŃ»·×éŅĄ“ĪŃ»·£¬ŌŁÓĆ2017³żŅŌ3£¬øł¾ŻÓąŹżµÄĒéæöČ·¶ØÓėµŚ¼øøöŹżĻąĶ¬¼“æÉµĆ½ā£»
£Ø2£©æÉĻČ¼ĘĖć³öÕāČżøöŹżµÄŗĶ£¬ŌŁ°“ÕÕ¹ęĀɼĘĖć£®
£Ø3£©ÓÉÓŚŹĒČżøöŹżÖŲø“³öĻÖ£¬Ņņ“ĖæÉÓĆĒ°ČżøöŹżµÄÖŲø“¶ą“Ī¼ĘĖć³ö½į¹ū£®
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø![]() £©”ßČĪŅāČżøöĻąĮŚøń×ÓÖŠĖłĢīµÄÕūŹżÖ®ŗĶ¶¼ĻąµČ£¬”ą±ķøńÖŠ“Ó×óĻņÓŅČżøöŹż×ÖŅ»øöŃ»·£¬”ą
£©”ßČĪŅāČżøöĻąĮŚøń×ÓÖŠĖłĢīµÄÕūŹżÖ®ŗĶ¶¼ĻąµČ£¬”ą±ķøńÖŠ“Ó×óĻņÓŅČżøöŹż×ÖŅ»øöŃ»·£¬”ą![]() £¬
£¬ ![]() £¬
£¬ ![]() £¬”ą
£¬”ą![]() £¬”ąµŚ
£¬”ąµŚ![]() øöøń×ÓÖŠĢīµÄŹżŹĒ
øöøń×ÓÖŠĢīµÄŹżŹĒ![]() £®
£®
£Ø![]() £©ÄÜ£¬
£©ÄÜ£¬ ![]() £®”ß
£®”ß![]() £»
£» ![]() £»ÓĆ
£»ÓĆ![]() £®
£®
µ±Ē°![]() øöøń×ÓÖŠµÄŹżµÄŗĶŹĒ
øöøń×ÓÖŠµÄŹżµÄŗĶŹĒ![]() £¬”ą¶ąŅ»øöøń×ÓŹżµÄŗĶŹĒ
£¬”ą¶ąŅ»øöøń×ÓŹżµÄŗĶŹĒ![]() £¬ŌŁ¶ąŅ»øöøń×ӵďżµÄŗĶŹĒ
£¬ŌŁ¶ąŅ»øöøń×ӵďżµÄŗĶŹĒ![]() ·ūŗĻĢāŅā£¬ĖłŅŌ
·ūŗĻĢāŅā£¬ĖłŅŌ![]() µÄÖµŹĒ
µÄÖµŹĒ![]() £®
£®
£Ø![]() £©”ßČ”Ē°
£©”ßČ”Ē°![]() øń×ÓÖŠµÄČĪŅāĮ½øöŹż£¬¼Ē×÷
øń×ÓÖŠµÄČĪŅāĮ½øöŹż£¬¼Ē×÷![]() £¬
£¬ ![]() £¬ĒŅ
£¬ĒŅ![]() £¬”ąĖłÓŠ
£¬”ąĖłÓŠ![]() µÄŗĶĪŖ£ŗ
µÄŗĶĪŖ£ŗ ![]() £®”ßÓÉÓŚČżøöŹżÖŲø“³öĻÖ£¬ÄĒĆ“Ē°
£®”ßÓÉÓŚČżøöŹżÖŲø“³öĻÖ£¬ÄĒĆ“Ē°![]() øń×ÓÖŠÕāČżøöŹż
øń×ÓÖŠÕāČżøöŹż![]() ³öĻÖĮĖ
³öĻÖĮĖ![]() “Ī£¬
“Ī£¬ ![]() ŗĶ
ŗĶ![]() ø÷³öĻÖĮĖ
ø÷³öĻÖĮĖ![]() “Ī£¬”ą“śČėŹ½×ÓæɵĆ
“Ī£¬”ą“śČėŹ½×ÓæɵĆ![]() £¬
£¬
“š£ŗ ![]() ½į¹ūĪŖ
½į¹ūĪŖ![]() £¬ĖłÓŠµÄ
£¬ĖłÓŠµÄ![]() µÄŗĶĪŖ
µÄŗĶĪŖ![]() £®
£®


 ³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬EŹĒABµÄÖŠµć£¬ĒŅDE”ĶAB£¬AB=10£¬Ōņ”ĻABC= £¬ ¶Ō½ĒĻßACµÄ³¤ĪŖ £® 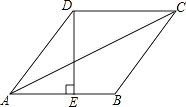
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĆęµÄĢāÄæ¼°·ÖĪö¹ż³Ģ£¬²¢°“ŅŖĒó½ųŠŠÖ¤Ć÷£® ŅŃÖŖ£ŗČēĶ¼£¬EŹĒBCµÄÖŠµć£¬µćAŌŚDEÉĻ£¬ĒŅ”ĻBAE=”ĻCDE£®
ĒóÖ¤£ŗAB=CD£®
·ÖĪö£ŗÖ¤Ć÷Į½ĢõĻ߶ĪĻąµČ£¬³£ÓƵÄŅ»°ć·½·ØŹĒÓ¦ÓĆČ«µČČż½ĒŠĪ»ņµČŃüČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬¹Ū²ģ±¾ĢāÖŠŅŖÖ¤Ć÷µÄĮ½ĢõĻ߶Ī£¬ĖüĆĒ²»ŌŚĶ¬Ņ»øöČż½ĒŠĪÖŠ£¬ĒŅĖüĆĒ·Ö±šĖłŌŚµÄĮ½øöČż½ĒŠĪŅ²²»Č«µČ£®Ņņ“Ė£¬ŅŖÖ¤AB=CD£¬±ŲŠėĢķ¼ÓŹŹµ±µÄøØÖśĻߣ¬¹¹ŌģČ«µČČż½ĒŠĪ»ņµČŃüČż½ĒŠĪ£®
ĻÖøų³öČēĻĀČżÖÖĢķ¼ÓøØÖśĻߵķ½·Ø£¬ĒėČĪŅāŃ”ŌńĘäÖŠŅ»ÖÖ£¬¶ŌŌĢā½ųŠŠÖ¤Ć÷£®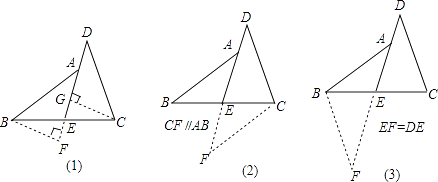
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūŅ»øöĄāÖł¹²ÓŠ15ĢõĄā£¬ÄĒĆ“ĖüµÄµ×ĆęŅ»¶ØŹĒ±ßŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĮŠ¼øøöĆüĢā£ŗ¢ŁĻąµČµÄ½ĒŹĒ¶Ō¶„½Ē£»¢ŚĶ¬Ī»½Ē¶¼ĻąµČ£»¢ŪČżøö½ĒĻąµČµÄČż½ĒŠĪŹĒµČ±ßČż½ĒŠĪ£»¢ÜĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£»¢ŻČōa2£½b2£¬Ōņa£½b.ĘäÖŠÕęĆüĢāµÄøöŹżÓŠ(””””)
A. 0øö B. 1øö C. 2øö D. 3øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŹżÖįÉĻČżµćA£¬O£¬B±ķŹ¾µÄŹż·Ö±šĪŖ6£¬0£¬£4£¬¶ÆµćP“ÓA³ö·¢£¬ŅŌĆæĆė6øöµ„Ī»µÄĖŁ¶ČŃŲŹżÖįĻņ×óŌČĖŁŌĖ¶Æ.
£Ø1£©µ±µćPµ½µćAµÄ¾ąĄėÓėµćPµ½µćBµÄ¾ąĄėĻąµČŹ±£¬µćPŌŚŹżÖįÉĻ±ķŹ¾µÄŹżŹĒ £»
£Ø2£©ĮķŅ»¶ÆµćR“ÓB³ö·¢£¬ŅŌĆæĆė4øöµ„Ī»µÄĖŁ¶ČŃŲŹżÖįĻņ×óŌČĖŁŌĖ¶Æ£¬ČōµćP”¢RĶ¬Ź±³ö·¢£¬ĪŹµćPŌĖ¶Æ¶ąÉŁŹ±¼ä×·ÉĻµćR£æ
£Ø3£©ČōMĪŖAPµÄÖŠµć£¬NĪŖPBµÄÖŠµć£¬µćPŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪMNµÄ³¤¶ČŹĒ·ń·¢Éś±ä»Æ£æČō·¢Éś±ä»Æ£¬ĒėÄćĖµĆ÷ĄķÓÉ£»Čō²»±ä£¬ĒėÄć»³öĶ¼ŠĪ£¬²¢Ēó³öĻ߶ĪMNµÄ³¤¶Č.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅåŠĀŌĖĖć”°”ł”±£¬¹ęŌņ£ŗa”łb=ab©a©b£¬Čē1”ł2=1”Į2©1©2=©1£¬Čōx2+x©1=0µÄĮ½øłĪŖx1 £¬ x2 £¬ Ōņx1”łx2= £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµ½Čż½ĒŠĪČżøö¶„µć¾ąĄėĻąµČµÄµćŹĒ£Ø £©
A. Čż½ĒŠĪČżĢõ½ĒĘ½·ÖĻߵĽ»µć B. Čż½ĒŠĪµÄČżĢõÖŠĻߵĽ»µć
C. Čż½ĒŠĪČż±ß“¹Ö±Ę½·ÖĻߵĽ»µć D. Čż½ĒŠĪČżĢõøßĻߵĽ»µć
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com