
| A. | k<-1 | B. | 1<k<2 | C. | k<1 | D. | -1<k<1 |
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{2}{3}$ | B. | x<$\frac{3}{2}$ | C. | x>-$\frac{3}{2}$ | D. | x<-$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
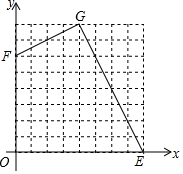 如图,在平面直角坐标系xOy中,E(8,0),F(0,6).
如图,在平面直角坐标系xOy中,E(8,0),F(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
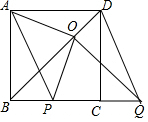 已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.
已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
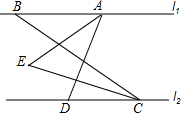 如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
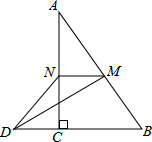 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
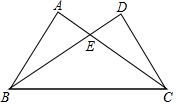 如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )| A. | ∠D=60° | B. | ∠DBC=40° | C. | AC=DB | D. | BE=10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com