
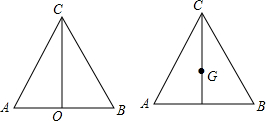
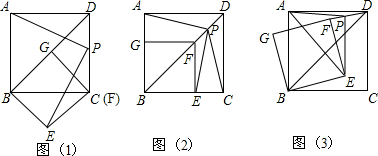
分析 (1)根据等腰三角形三线合一的性质求出AO的长,利用勾股定理求AG,则CG与AG的和就是点P的运动距离;
(2)作辅助线构建最短距离AH,因为点P在CG与AG的速度不同,因此要构建同速度的最短距离AH,满足k=$\frac{CG}{GH}$=2,求出这时的CG和AG,代入速度计算时间即可;
(3)与(2)同理,作辅助线构建最短距离AH,满足k=$\frac{CG}{GH}$,利用同角三角函数求出结论.
解答 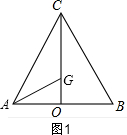 解:(1)如图1,∵CO=3$\sqrt{3}$,CG=2$\sqrt{3}$,
解:(1)如图1,∵CO=3$\sqrt{3}$,CG=2$\sqrt{3}$,
∴OG=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$,
∵△ABC是等腰三角形,CO是高,
∴AO=BO=$\frac{1}{2}$AB=3,
由勾股定理得:AG=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
∴点P的运动距离=AG+CG=2$\sqrt{3}$+2$\sqrt{3}$=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$;
(2)如图2,过点A作AH⊥BC于点H,交CO于点G,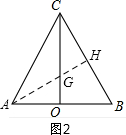
∵tan∠CAB=$\frac{OC}{AO}$=$\frac{3\sqrt{3}}{3}$=$\sqrt{3}$,
∴∠CAB=60°,
∴△ABC是等边三角形,
∵CO⊥AB,
∴∠OCB=30°,则GH=$\frac{1}{2}$GC,
最短距离AH=3$\sqrt{3}$,OG=$\sqrt{3}$,CG=2$\sqrt{3}$,AG=2$\sqrt{3}$,
∴t最小值=$\frac{2\sqrt{3}}{2}$+2$\sqrt{3}$=3$\sqrt{3}$;
(3)如图3,过点A作AH⊥BC于点H,交CO于点G,
∵∠HAB=∠OCB,
tan∠HAB=tan∠OCB=$\frac{3}{6}$=$\frac{1}{2}$,
∴$\frac{OG}{AO}=\frac{1}{2}$,
∴$\frac{OG}{3}=\frac{1}{2}$,
∴OG=$\frac{3}{2}$,
则AG=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
∴k=$\frac{CG}{GH}=\frac{AG}{OG}$=$\frac{\frac{3\sqrt{5}}{2}}{\frac{3}{2}}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$,$\frac{3}{2}$.
点评 本题是三角形的综合题,考查了等腰三角形的性质,重点考查了等腰三角形三线合一的性质,利用动点问题把行程问题与几何问题结合起来;如果求最短时间,速度不同,要化成同速度来求最小值.


科目:初中数学 来源: 题型:解答题
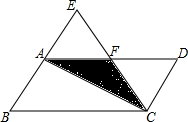 如图,在平行四边形ABCD中,BC=6cm,将△ABC沿对角线AC折叠,点B的对应点落在点E处,BC边的对应边CE与AD边交于点F,此时△CDF为等边三角形.
如图,在平行四边形ABCD中,BC=6cm,将△ABC沿对角线AC折叠,点B的对应点落在点E处,BC边的对应边CE与AD边交于点F,此时△CDF为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

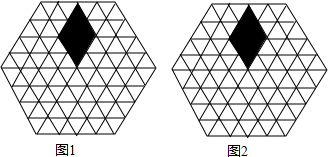
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
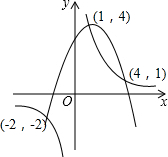 二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )
二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )| A. | 1<x<4或x<-2 | B. | 1<x<4或-2<x<0 | ||
| C. | 0<x<1或x>4或-2<x<0 | D. | -2<x<1或x>-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
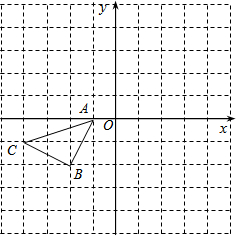 操作题
操作题查看答案和解析>>
科目:初中数学 来源: 题型:选择题
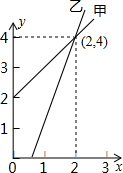 如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:
如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:| A. | ①② | B. | ②③ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com