
分析 根据题目中数据可以发现奇数个数和偶数个数分别具有一定的规律性,从而可以解答本题.
解答 解:∵2,-2$\frac{3}{4}$,3$\frac{2}{3}$,-4$\frac{5}{8}$,5$\frac{3}{5}$,-6$\frac{7}{12}$…,
∴当n=2k-1且k为不小于1的整数时,第n个数是:(2k-1)$\frac{k}{2k-1}$,
当n=2k且k为不小于1的整数时,第n个数是:-2k$\frac{2k+1}{4k}$,
故答案为:$\left\{\begin{array}{l}{(2k-1)\frac{k}{2k-1}}&{k≥1且为整数}\\{-2k\frac{2k+1}{4k}}&{k≥1且k为整数}\end{array}\right.$.
点评 本题考查数字的变化类,解题的关键是明确题意,发现其中的变化规律.


科目:初中数学 来源: 题型:填空题
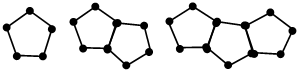 用火柴棒按如图的方式搭五边形组成的图形
用火柴棒按如图的方式搭五边形组成的图形| 五边形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com