
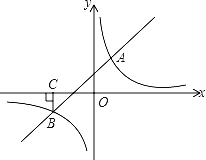
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标.
【答案】(1)y=![]() ;(2)点P的坐标为(﹣8,﹣
;(2)点P的坐标为(﹣8,﹣![]() ),(2,3).
),(2,3).
【解析】
(1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;
(2)由B点(-3,n)在反比例函数y=![]() 的图象上,于是得到B(-3,-2),求得BC=2,设△PBC在BC边上的高为h,根据三角形的面积公式列方程即可得到结论.
的图象上,于是得到B(-3,-2),求得BC=2,设△PBC在BC边上的高为h,根据三角形的面积公式列方程即可得到结论.
(1)∵反比例函数y=![]() 的图象经过点A(2,3),
的图象经过点A(2,3),
∴m=6.
∴反比例函数的解析式是y=![]() ;
;
(2)∵B点(﹣3,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=﹣2,
∴B(﹣3,﹣2),
∴BC=2,设△PBC在BC边上的高为h,
则![]() BCh=5,
BCh=5,
∴h=5,
∵P是反比例函数图象上的一点,
∴点P的横坐标为:﹣8或2,
∴点P的坐标为(﹣8,﹣![]() ),(2,3).
),(2,3).


科目:初中数学 来源: 题型:
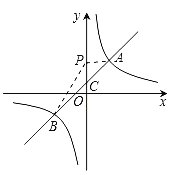
【题目】两条抛物线![]() 与
与![]() 的两个交点
的两个交点![]() 、
、![]() 都在
都在![]() 轴上,抛物线
轴上,抛物线![]() 的顶点为
的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(3)判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到点
,得到点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
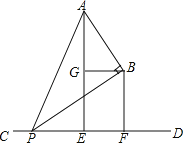
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
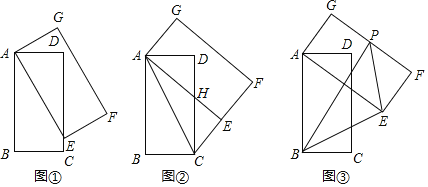
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
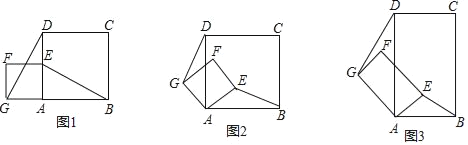
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为
,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为![]() ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
![]() 如图
如图![]() ,当点E落在DC边上时,直写出线段EC的长度为______;
,当点E落在DC边上时,直写出线段EC的长度为______;
![]() 如图
如图![]() ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 直接写出线段DH的长度为______.
直接写出线段DH的长度为______.
![]() 如图
如图![]() 设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,
设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
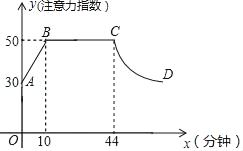
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
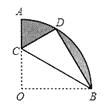
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com