
 已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.
已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积. 分析 根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=17.根据等腰三角形的性质得到AB=CD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
解答 解:(1)∵BE和CE分别平分∠ABC和∠BCD,
∵AB∥CD,∴∠ABC+∠DCB=180°,
∴$\frac{1}{2}$(∠ABC+∠DCB)=90°,
∴∠EBC+∠ECB=90°,
∴△EBC是直角三角形,
根据勾股定理:BC=17,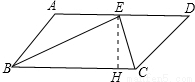
∵AD∥BC,
∴∠DEC=∠ECB,
∵∠ECD=∠ECB,
∴∠DEC=∠ECD,
∴DE=CD,
同理AB=AE.
∴AB+CD=AE+DE=AD=BC=17,
∴平行四边形ABCD周长=BC+AD+AB+CD=17+17+17=51.
(2)如图,作EH⊥BC,垂足为H.
S△BEC=$\frac{1}{2}$×15×8=60,
又∵S△BEC=$\frac{1}{2}$×BC×EH,
∴S平行四边形ABCD=BC×EH=2S△BEC=120.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 小明家 | 爷爷家 | |
| 屋顶收集雨水面积(m2) | 160 | 120 |
| 蓄水池容积(m3) | 50 | 13 |
| 蓄水池已有水量(m3) | 34 | 11.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
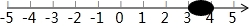 把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.
把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
若点P(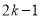 ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( )
A. 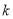 <
<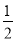 B.
B.  <2 C.
<2 C.  <
<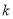 <2 D.
<2 D. 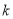 >2
>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com