
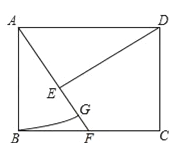
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=![]() ,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
试题解析:(1)∵四边形ABCD是矩形,∴∠B=90°,AD=BC,AD∥BC,∴∠DAE=∠AFB,∵DE⊥AF,∴∠AED=90°=∠B,在△ABF和△DEA中,∵∠AFB=∠DAE,∠B=∠DEA,AF=AD,∴△ABF≌△DEA(AAS),∴DE=AB;
(2)∵BC=AD,AD=AF,∴BC=AF,∵BF=1,∠ABF=90°,∴由勾股定理得:AB=![]() =
=![]() ,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=
,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=![]() ,∴扇形ABG的面积=
,∴扇形ABG的面积=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分12分) 如图1,在底面积为l00cm2、高为20cm的长方体水槽内放人一个圆柱形烧杯.以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h与注水时间t之间的函数关系如图2所示.
(1)写出函数图象中点A、点B的实际意义;
(2)求烧杯的底面积;
 (3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
(3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“爱护地球,绿化祖国”的创建活动中,组织了100名学生开展植树造林活动,其植树情况整理如下表:
植树棵树(单位:棵) | 4 | 5 | 6 | 8 | 10 |
人数(人) | 30 | 22 | 25 | 15 | 8 |
则这100名学生所植树棵树的中位数为( )
A. 4B. 5C. 5.5D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com