
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.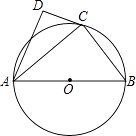
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
【答案】
(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4
(2)解:证明:连接OC
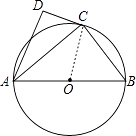
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.
【解析】(1)首先依据圆周角定理可得到∠ACB=90°,然后利用勾股定理求得AC的长即可;
(2)连接OC,首先利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,依据平行线的判定定理可得到OC∥AD,接下来,由AD⊥CD,可证明OC⊥CD,从而可证明CD是⊙O的切线.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.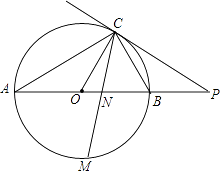
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.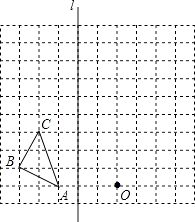
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
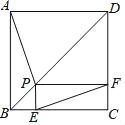
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )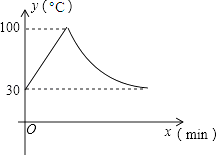
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
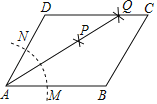
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com