
 ��ͼ������ABCD�У�AB=5��BD=13��Rt��EFG��ֱ�DZ�GE��CB���ӳ����ϣ�E����ص�B���أ���FGE=90�㣬FG=3��������ABCD�̶�����Rt��EFG��������BC�����˶�������Fǡ�þ���BDʱ������EFG�Ƶ�F��ʱ����ת���㣨0�㣼���㣼90�㣩������ת�еġ�EFGΪ��E��F��G�䣬����ת�����У���ֱ��E��G����ֱ��BC����N����ֱ��BD����M�㣬����BMNΪ��MNΪ�ױߵĵ���������ʱ��FM�ij�Ϊ3$\sqrt{26}$��
��ͼ������ABCD�У�AB=5��BD=13��Rt��EFG��ֱ�DZ�GE��CB���ӳ����ϣ�E����ص�B���أ���FGE=90�㣬FG=3��������ABCD�̶�����Rt��EFG��������BC�����˶�������Fǡ�þ���BDʱ������EFG�Ƶ�F��ʱ����ת���㣨0�㣼���㣼90�㣩������ת�еġ�EFGΪ��E��F��G�䣬����ת�����У���ֱ��E��G����ֱ��BC����N����ֱ��BD����M�㣬����BMNΪ��MNΪ�ױߵĵ���������ʱ��FM�ij�Ϊ3$\sqrt{26}$�� ���� ��ͼ����BRƽ�֡�DBC��CD��R��RT��BD����ΪT�����RT��RC�����á�BTR�ס�MG��F��$\frac{FM}{BR}=\frac{FG��}{RT}$���г����̼��ɽ����
��� �⣺��ͼ����BRƽ�֡�DBC��CD��R��RT��BD����ΪT��
���ı���ABCD�Ǿ��Σ�
��AB=CD=5����C=90�㣬
��BD=13��
��BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12��
�ڡ�BRT�͡�BRC�У�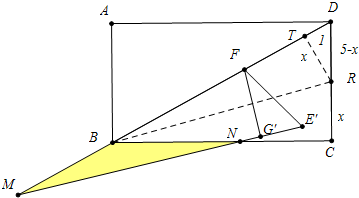
$\left\{\begin{array}{l}{��C=��BTR}\\{��RBT=��RBC}\\{BR=BR}\end{array}\right.$��
���BRT�ա�BRC��
��BT=BC=12��TD=1����RT=RC=x��
��RT��RTD����TD2+RT2=RD2��
��x2+12=��5-X��2��
��x=$\frac{12}{5}$��
��BR=$\sqrt{B{T}^{2}+R{T}^{2}}$=$\sqrt{1{2}^{2}+��\frac{12}{5}��^{2}}$=$\frac{12\sqrt{26}}{5}$��
��BN=BM��
���BMN=��BNM��
�ߡ�DBC=��BMN+��BNM����RBD=��RBC��
���TBR=��FMG�䣬
�ߡ�RTB=��FG��M=90�㣬
���BTR�ס�MG��F��
��$\frac{FM}{BR}=\frac{FG��}{RT}$��
��$\frac{FM}{\frac{12\sqrt{26}}{5}}=\frac{3}{\frac{12}{5}}$��
��FM=3$\sqrt{26}$��
���� ���⿼����ε����ʡ���ת�����ʡ����ɶ�������ƽ���ߵ����ʣ�ȫ�������ε��ж������ʡ����������ε��ж������ʣ���ȷ����ͼ���ǽ���Ĺؼ���


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 3 | C�� | -3��3 | D�� | -3��-7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=x2+bx+c��y�ύ�ڵ�C����x�ύ�ڵ�A��B����AB=2�������ߵĶԳ���Ϊֱ��x=2��
��ͼ����֪������y=x2+bx+c��y�ύ�ڵ�C����x�ύ�ڵ�A��B����AB=2�������ߵĶԳ���Ϊֱ��x=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
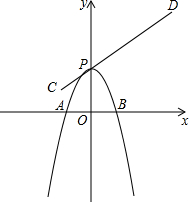 ��ͼ����������x���ཻ��A��B���㣬�ڱ��������ߵ���״���С�����ǰ���£�����P���߶�CD���ƶ�����C��D������ֱ�Ϊ��-1��1���ͣ�3��4����������P�ƶ�����Cʱ����Bǡ����ԭ���غϣ��������ƶ������У���A�ƶ��ľ���Ϊ��������
��ͼ����������x���ཻ��A��B���㣬�ڱ��������ߵ���״���С�����ǰ���£�����P���߶�CD���ƶ�����C��D������ֱ�Ϊ��-1��1���ͣ�3��4����������P�ƶ�����Cʱ����Bǡ����ԭ���غϣ��������ƶ������У���A�ƶ��ľ���Ϊ��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
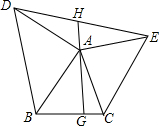 ��ͼ���ڡ�ABC�У���AΪ���㣬��AB��ACΪֱ�������ε�ֱ�DZ������������ֱ�������Σ�����DE����A����BC������AG�������ӳ�AG��DE��H��
��ͼ���ڡ�ABC�У���AΪ���㣬��AB��ACΪֱ�������ε�ֱ�DZ������������ֱ�������Σ�����DE����A����BC������AG�������ӳ�AG��DE��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3a+b=3ab | B�� | -a2b+2a2b=a2b | C�� | 2a3+3a2=5a5 | D�� | 3a-a=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com