【题目】小刚在实践课上要做一个如图1所示的折扇，折扇扇面的宽度AB是骨柄长OA的
，折扇张开的角度为120°．小刚现要在如图2所示的矩形布料上剪下扇面，且扇面不能拼接，已知矩形布料长为24
cm，宽为21cm．小刚经过画图、计算，在矩形布料上裁剪下了最大的扇面，若不计裁剪和粘贴时的损耗，此时扇面的宽度AB为（ ）
A． 21cm B．20 cm C． 19cm D． 18cm
字词句段篇系列答案科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中，O为坐标原点，直线y＝kx+b经过点A（﹣2，﹣1），交y轴负半轴于点B，且∠ABO＝30°，过点A作直线AC⊥x轴于点C，点P在直线AC上．
（1）k＝ ；b＝ ；
（2）设△ABP的面积为S，点P的纵坐标为m．
①当m＞0时，求S与m之间的函数关系式；
②当S＝2时，求m的值；
③当m＞0且S＝4时，以BP为边作等边△BPQ，请直接写出符合条件的所有点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=﹣
+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知B点的坐标为B（8，0）．
（1）求抛物线的解析式及其对称轴方程．
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由．
（3）在抛物线上BC之间是否存在一点D，使得△DBC的面积最大？若存在请求出点D的坐标和△DBC的面积；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在四边形ABCD中，AD//BC，对角线AC、BD交于点O，且AC=BD，下列四个命题中真命题是（ ）
A. 若AB=CD，则四边形ABCD一定是等腰梯形；
B. 若∠DBC=∠ACB，则四边形ABCD一定是等腰梯形；
C. 若
，则四边形ABCD一定是矩形；
D. 若AC⊥BD且AO=OD，则四边形ABCD一定是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y=kx+b交x轴于点A，交y轴于点B，直线y=2x﹣4交x轴于点D，与直线AB相交于点C（3，2）．
（1）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集；
（2）若点A的坐标为（5，0），求直线AB的解析式；
（3）在（2）的条件下，求四边形BODC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A，B两点，点A在点B的左侧．
（1）如图1，当k=1时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），在直线y=kx+1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角三角板
放在平面直角坐标系中，直角边
垂直
轴，垂足为
，已知
，点
，
，
均在反比例函数
的图象上，分别作
轴于
，
轴于
，延长
，
交于点
，且点为
的中点．
求点
的坐标；
求四边形
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
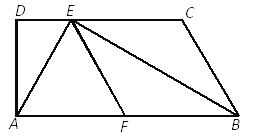
【题目】如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB的中点，联结AE、EF，且AE⊥BE．
求证：（1）四边形BCEF是菱形；
（2）
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
