
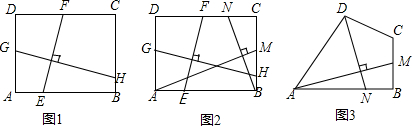
分析 (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题;
(2)只需运用(1)中的结论,就可得到$\frac{EF}{GH}$=$\frac{AD}{AB}$=$\frac{BN}{AM}$,就可解决问题;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得$\frac{DN}{AM}$=$\frac{AR}{AB}$.设SC=x,DS=y,则AR=BS=5+x,RD=10-y,在Rt△CSD中根据勾股定理可得x2+y2=25①,在Rt△ARD中根据勾股定理可得(5+x)2+(10-y)2=100②,解①②就可求出x,即可得到AR,问题得以解决.
解答 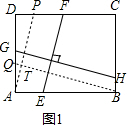 解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴$\frac{AP}{BQ}$=$\frac{AD}{AB}$,
∴$\frac{EF}{GH}$=$\frac{AD}{AB}$;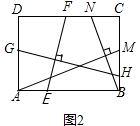
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得$\frac{EF}{GH}$=$\frac{AD}{AB}$,$\frac{BN}{AM}$=$\frac{AD}{AB}$,
∴$\frac{BN}{AM}$=$\frac{EF}{GH}$=$\frac{11}{15}$.
故答案为$\frac{11}{15}$;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,
则四边形ABSR是平行四边形.
∵∠ABC=90°,∴?ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得$\frac{DN}{AM}$=$\frac{AR}{AB}$.
设SC=x,DS=y,则AR=BS=5+x,RD=10-y,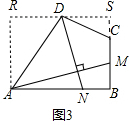
∴在Rt△CSD中,x2+y2=25①,
在Rt△ARD中,(5+x)2+(10-y)2=100②,
由②-①得x=2y-5③,
解方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=25}\\{x=2y-5}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-5}\\{y=0}\end{array}\right.$(舍去),或$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴AR=5+x=8,
∴$\frac{DN}{AM}$=$\frac{AR}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题主要考查了矩形的判定与性质、相似三角形的判定与性质、勾股定理、解二元二次方程组等知识,运用(1)中的结论是解决第(2)、(3)小题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
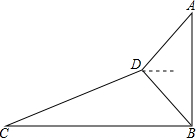 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
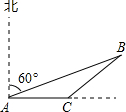 三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
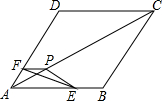 如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
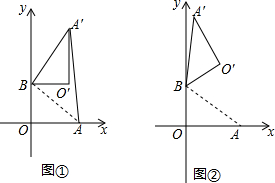
 已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3
已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com