
【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备,现要将这些设备全部运往A、B两市,其中运往A市18台、运往B市14台,从甲地运往A、B两市的费用分别为800元/台和500元/台,从乙地运往A、B两市的费用分别为700元/台和600元/台.设甲地运往A市的设备有x台.
(1)请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数;
(2)求出总运费y(元)与x(台) 的函数关系式,并求出自变量的取值范围;
(3)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案,哪种方案总运费最小,最小值是多少?
【答案】
(1)解:甲地运往B市的设备有(17﹣x)台,
乙地运往A市的设备有(18﹣x)台,
乙地运往B市的设备有15﹣(18﹣x)=(x﹣3)台
(2)解:根据题意得:y=800x+500(17﹣x)+700(18﹣x)+600(x﹣3),
即y=200x+19300.
由 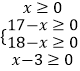 ,解得3≤x≤17.
,解得3≤x≤17.
∴自变量的取值范围是:x为正整数且3≤x≤17
(3)解:∵要使总运费不高于20200元,
∴200x+19300≤20200,
解得:x≤4.5.(8分)
又∵x为正整数且3≤x≤17,
∴x=3或4.
∴该公司调配方案有两种:
方案一:甲地运往A市3台,运往B市14台,乙地运往A市15台,运往B市0台;
方案二:甲地运往A市4台,运往B市13台,乙地运往A市14台,运往B市1台;
∵在y=200x+19300中,k=200>0,
∴y随x的增大而增大,
∴当x=3时,总运费最小,最小值是y=200×3+19300=19900(元).
即甲地运往A市3台,运往B市14台,乙地运往A市15台,运往B市0台总运费最小,最小值是19900元
【解析】(1)根据调配方案,即可解决问题.(2)根据每台的运费即可得出函数关系式;利用不等式求出自变量的取值范围.(3)列出不等式,求整数解,利用一次函数的性质确定最小值.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( ) 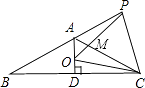
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力 | 科研能力 | 组织能力 | |
甲 | 81 | 85 | 86 |
乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在⊙O上,DE⊥OA,DF⊥OB,垂足分别为E,F,若∠EDF=50°,则∠C的度数为( ) 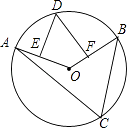
A.40°
B.50°
C.65°
D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向,B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(5)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com