练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】心理学家发现：课堂上，学生对概念的接受能力s与提出概念的时间t（单位：min）之间近似满足函数关系s＝at2+bt+c（a≠0），s值越大，表示接受能力越强．如图记录了学生学习某概念时t与s的三组数据，根据上述函数模型和数据，可推断出当学生接受能力最强时，提出概念的时间为（　　）

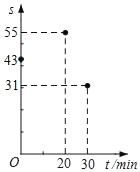
    A. 8min B. 13min C. 20min D. 25min

    【答案】B

    【解析】

    先利用条件求出解析式，再变式求出最值即可解答.

    解：已知满足函数关系s＝at2＋bt＋c（a≠0），

    根据图像可知经过（0,43），（20,55），（30,31），

    将已知点代入解析式得s＝－0.1＋2.6t＋43,

    根据函数性质得t＝－＝13时，s最大，

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有A、B两组卡片共5张，A组的三张分别写有数字2，4，6，B组的两张分别写有3，5．它们除了数字外没有任何区别，

    （1）随机从A组抽取一张，求抽到数字为2的概率；

    （2）随机地分别从A组、B组各抽取一张，请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则：若选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

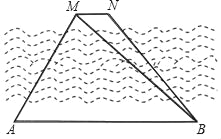
    【题目】如图，在一条河的北岸有两个目标M、N，现在位于它的对岸设定两个观测点A、B．已知AB∥MN，在A点测得∠MAB＝60°，在B点测得∠MBA＝45°，AB＝600米．

    (1)求点M到AB的距离；（结果保留根号）

    (2)在B点又测得∠NBA＝53°，求MN的长．（结果精确到1米）

    （参考数据：≈1.732，sin53°≈0.8，cos53°≈0.6，tan53°≈1.33，cot53°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了预防疾病，某单位对办公室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例，药物燃烧后，y与x成反比例(如图)，现测得药物8分钟燃毕，此时室内空气中每立方米的含药量6毫克，请根据题中所提供的信息，解答下列问题：

    (1)药物燃烧时，y关于x的函数关系式为________，自变量x的取值范为________；药物燃烧后，y关于x的函数关系式为________．

    (2)研究表明，当空气中每立方米的含药量低于1.6毫克时员工方可进办公室，那么从消毒开始，至少需要经过________分钟后，员工才能回到办公室；

    (3)研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

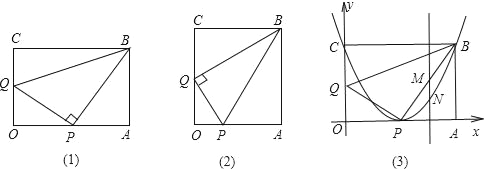
    【题目】如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．

    （1）如图（1），若∠BPQ＝90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．

    （2）若∠PQB＝90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA＝2：3．

    （3）在（1）中，若OA＝8，OC＝8，OP＝CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．

    ①求此抛物线的解析式．

    ②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线型拱桥，当拱顶离水面8m时，水面宽AB为12m．当水面上升6m时达到警戒水位，此时拱桥内的水面宽度是多少m？

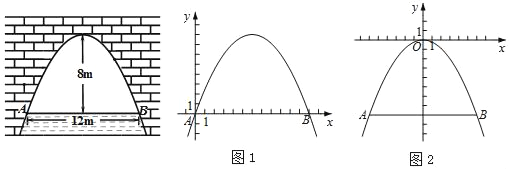
    下面给出了解决这个问题的两种方法，请补充完整：

    方法一：如图1，以点A为原点，AB所在直线为x轴，建立平面直角坐标系xOy，

    此时点B的坐标为（　 　，　 　），抛物线的顶点坐标为（　 　，　 　），

    可求这条抛物线所表示的二次函数的解析式为　 　．

    当y＝6时，求出此时自变量x的取值，即可解决这个问题．

    方法二：如图2，以抛物线顶点为原点，对称轴为y轴，建立平面直角坐标系xOy，

    这时这条抛物线所表示的二次函数的解析式为　 　．

    当y＝　 　时，求出此时自变量x的取值为　 　，即可解决这个问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

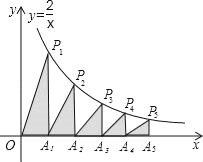
    【题目】如图，在x轴的正半轴上依次截取OA1＝A1A2＝A2A3＝A3A4＝A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y＝（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2，A2P3A3，A3P4A4，A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S10＝_____．（n≥1的整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形OABC在平面直角坐标系中，若x2﹣2x+2＝0的两根是x1、x2，且OC＝x1+x2，OA＝x1x2

    （1）求B点的坐标．

    （2）把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求直线BD的解析式．

    （3）在平面上是否存在点P，使D、C、B、P四点形成的四边形为平形四边形？若存在，请直接写出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体，如图所示．

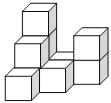
    （1）这个几何体由 个小正方体组成，请画出这个几何体的三视图；

    （2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 个正方体只有一个面是黄色，有 个正方体只有两个面是黄色，有 个正方体只有三个面是黄色；

    （3）若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方体．

    查看答案和解析>>

    同步练习册答案