
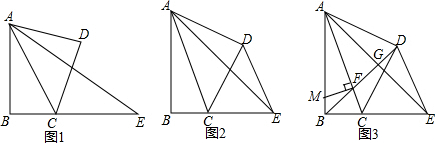
分析 (1)首先证明∠D=90°,再证明∠BAE=∠CAD,由∠BAE+∠E=90°,∠ACD+∠CAD=90°,即可推出∠E=∠ACD;
(2)如图2中,取AC的中点O,连接OB、OD,作DN⊥BE于N,DM⊥AB于M.首先证明A、B、C、D四点共圆,再证明△DMA≌△DNC,△DBA≌△DBE,即可解决问题;
(3)由△AFM∽△ABC,可得$\frac{AM}{AC}$=$\frac{FM}{CB}$,推出FM•AC=15×6=90,设FM=a,则AC=$\frac{90}{a}$,连接CM,同法可知B、C、F、M四点共圆,可得∠FMC=∠FBC=45°=∠FCM,推出FM=CF=a,在Rt△AFM中,由AM2=AF2+FM2,可得152=a2+($\frac{90}{a}$-a)2,解得a=$\frac{3\sqrt{10}}{2}$或6$\sqrt{5}$(舍弃),推出AC=6$\sqrt{10}$,AF=$\frac{9\sqrt{10}}{2}$,AD=6$\sqrt{5}$,由△ADF∽△BCF可得$\frac{AD}{BC}$=$\frac{DF}{CF}$,由此即可解决问题.
解答 (1)证明:如图1中,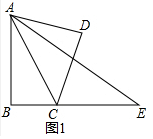
∵∠BAD+∠BCD=180°,∠B=90°,
∴∠D=360°-180°-90°=90°,
∵∠BAC=∠DAE,
∴∠BAE=∠CAD,
∵∠BAE+∠E=90°,∠ACD+∠CAD=90°,
∴∠E=∠ACD.
(2)证明:如图2中,取AC的中点O,连接OB、OD,作DN⊥BE于N,DM⊥AB于M.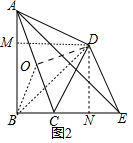
∵△ABC,△ADC都是直角三角形,OA=OC,
∴OB=OA=OC=OD,
∴A、B、C、D四点共圆,
∵AB=BE,
∴∠ACD=∠E=45°,
∴∠ABD=∠ACD=45°,∵∠ABC=90°,
∴∠DBA=∠DBE,
∵DN⊥BE,DM⊥AB,
∴DM=DN,则四边形BMDN是正方形,
∴∠MDN=∠ADC=90°,
∴∠ADM=∠CDN,
在△DMA和△DNC中,
$\left\{\begin{array}{l}{∠ADM=∠CDN}\\{DM=DN}\\{∠DMA=∠DNC}\end{array}\right.$,
∴△DMA≌△DNC,
∴AD=DC,
在△DBA和△DBE中,
$\left\{\begin{array}{l}{BD=BD}\\{∠DBA=∠DBE}\\{BA=BE}\end{array}\right.$,
∴△DBA≌△DBE,
∴DA=DE,
∴DC=DE.
(3)解:如图3中,
∵∠MAF=∠BAC,∠AFM=∠ABC=90°,
∴△AFM∽△ABC,
∴$\frac{AM}{AC}$=$\frac{FM}{CB}$,
∴FM•AC=15×6=90,设FM=a,则AC=$\frac{90}{a}$,
连接CM,同法可知B、C、F、M四点共圆,可得∠FMC=∠FBC=45°=∠FCM,
∴FM=CF=a,
在Rt△AFM中,∵AM2=AF2+FM2,
∴152=a2+($\frac{90}{a}$-a)2,
解得a=$\frac{3\sqrt{10}}{2}$或6$\sqrt{5}$(舍弃),
∴AC=6$\sqrt{10}$,AF=$\frac{9\sqrt{10}}{2}$,AD=6$\sqrt{5}$,
由△ADF∽△BCF可得$\frac{AD}{BC}$=$\frac{DF}{CF}$,
∴$\frac{6\sqrt{5}}{6}$=$\frac{DF}{\frac{3\sqrt{10}}{2}}$,
∴DF=$\frac{15\sqrt{2}}{2}$.
点评 本题考查四边形综合题、等腰直角三角形的性质、四点共圆、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会证明四点共圆解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
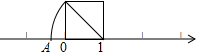 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | -$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | -1-$\sqrt{2}$ | D. | -1+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
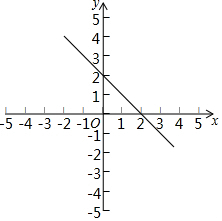 在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.
在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
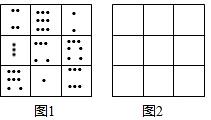 有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).
有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com