
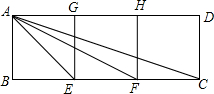
 如图,矩形ABCD是由三个完全相同的正方形ABEG、GEFH、HFCD组成的,证明:△FEA∽△AEC.
如图,矩形ABCD是由三个完全相同的正方形ABEG、GEFH、HFCD组成的,证明:△FEA∽△AEC. 分析 设三个完全相同的正方形ABEG、GEFH、HFCD的边长为a,由勾股定理求出AE,求出$\frac{AE}{EF}$=$\frac{EC}{AE}$,再由公共角∠AEF=∠CEA,即可得出△FEA∽△AEC.
解答 证明:设三个完全相同的正方形ABEG、GEFH、HFCD的边长为a,
由勾股定理得:AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a,
∴$\frac{AE}{EF}$=$\frac{\sqrt{2}a}{a}$=$\sqrt{2}$,$\frac{EC}{AE}$=$\frac{2a}{\sqrt{2}a}$=$\sqrt{2}$,
∴$\frac{AE}{EF}$=$\frac{EC}{AE}$,
又∵∠AEF=∠CEA,
∴△FEA∽△AEC.
点评 本题考查了正方形的性质、勾股定理、相似三角形的判定;熟练掌握正方形的性质和相似三角形的判定方法,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
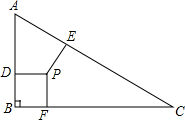 某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?
某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com