
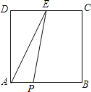
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为正方形
为正方形![]() 边上的动点,动点
边上的动点,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,若点
运动,若点![]() 经过的路程为
经过的路程为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)当点![]() 运动路程为多少时,
运动路程为多少时,![]() 的面积为
的面积为![]() .
.
【答案】(1)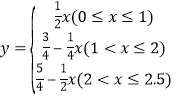 ;(2)点
;(2)点![]() 运动路程为
运动路程为![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() .
.
【解析】
(1)分别从0≤x≤1,1<x≤2,2<x≤2.5去分析求解即可求得答案;
(2)分别从0≤x≤1,1<x≤2,2<x≤2.5时,y![]() ,去求解即可求得答案.
,去求解即可求得答案.
(1)①当0≤x≤1时,AP=x,AD=1,则y![]() x×1
x×1![]() x;
x;
②如图(2),当1<x≤2时,BP=x﹣1,CP=2﹣x,∴y=S梯形ABCE﹣S△ABP﹣S△CPE![]() (
(![]() 1)×1
1)×1![]() 1×(x﹣1)
1×(x﹣1)![]() (2﹣x)
(2﹣x)![]() x;
x;
③如图(3),当2<x≤2.5时,EP=2.5﹣x,∴y![]() (2.5﹣x)×1
(2.5﹣x)×1![]() x;
x;
综上所述: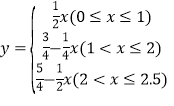 ;
;
(2)①当0≤x≤1时,![]() ,解得:x
,解得:x![]() ;
;
②当1<x≤2时,![]() ,解得:x
,解得:x![]() ;
;
③当2<x≤2.5时,![]() ,解得:x
,解得:x![]() (舍去);
(舍去);
综上:当点P运动路程为![]() 或
或![]() 时,△APE的面积为
时,△APE的面积为![]() .
.


科目:初中数学 来源: 题型:
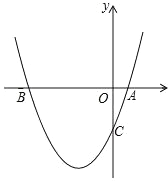
【题目】如图,已知二次函数 y=x2+bx+c 过点 A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)求△ABC 的面积;
(3)在抛物线上存在一点 P 使△ABP 的面积为 10,请求出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
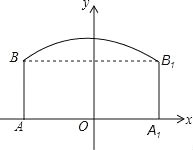
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
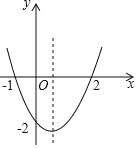
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
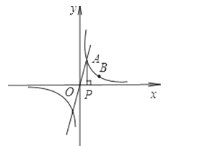
【题目】已知正比例函数y=2x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
(1)求反比例函数的解析式;
(2)如果点B为反比例函数在第一象限图象上的点(点B与点A不重合),且点B的横坐标为2,在x轴上求一点M,使MA+MB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com