
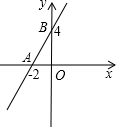
 如图,直线y=kx+b经过A、B两点.
如图,直线y=kx+b经过A、B两点.分析 (1)根据点A、B的坐标利用待定系数法即可求出直线AB的表达式;
(2)根据题意画出函数图象,由△OAM的面积为S,且3<S<5,找出点M坐标的范围,根据临界点的坐标和点A的坐标利用待定系数法即可找出k'和b'的取值范围.
解答 解:(1)将点A(-2,0)、B(0,4)代入y=kx+b中.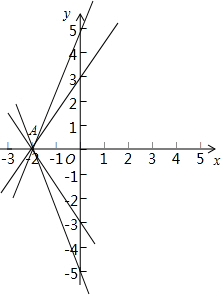
得:$\left\{\begin{array}{l}{b=4}\\{-2k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$,
直线表达式为y=2x+4.
(2)依照题意画出图形,如图所示.
设点M的坐标为(0,m),
S=$\frac{1}{2}$OA•yM=|m|,
∵3<S<5,即3<|m|<5,
解得:-5<m<-3或3<m<5.
取M的坐标为(0,-5)、(0,-3)、(0,3)、(0,5),结合点A(-2,0),
利用待定系数法即可得出:
$\frac{3}{2}$<k′<$\frac{5}{2}$,3<b′<5或-$\frac{5}{2}$<k′<-$\frac{3}{2}$,-5<b′<-3.
点评 本题考查了一次函数图象与几何变换以及待定系数法求函数解析式,解题的关键是:(1)利用待定系数法求出直线的解析式;(2)根据△OAM的面积找出点M纵坐标的范围.本题属于中档题,难度不大,解决该题型题目时,根据题意画出图形,利用数形结合解决问题是关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ | B. | 5$\sqrt{3}$+5$\sqrt{2}$=10$\sqrt{5}$ | C. | 4$\sqrt{3}$×2$\sqrt{2}$=8$\sqrt{6}$ | D. | 4$\sqrt{2}$÷2$\sqrt{2}$=2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 不变 | D. | 缩小为原来的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2xy+6xz+3=2x(y+3z)+3 | B. | (x+6)(x-6)=x2-36 | ||
| C. | -2x2-2xy=-2x(x+y) | D. | 3a2-3b2=3(a2-b2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)| 分组 | 频数 | 频率 |
| 156.5~161.5 | 3 | 0.15 |
| 161.5~166.5 | 2 | 0.10 |
| 166.5~171.5 | 4 | |
| 171.5~176.5 | 0.30 | |
| 176.5~181.5 | ||
| 合计 | 20 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.
在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com