
 根据图(1)所示的程序,得到了y与x的函数,其图象如图(2)所示.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.以下结论:
根据图(1)所示的程序,得到了y与x的函数,其图象如图(2)所示.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.以下结论:| 2 |
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| 2 |
| x |
| 4 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 4 |
| a2 |
| 2 |
| a |
| 4 |
| a2 |
| 4 |
| a2 |
| 4 |
| a2 |
| 8 |
| a2 |
| 8 |
| a2 |


科目:初中数学 来源: 题型:
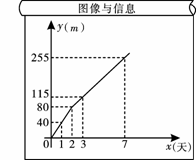
娄底至新化高速公路的路基工程分段招标,市路桥公司中标承包了一段路基工程,进入施工场地后,所挖筑路基的长度y(m)与挖筑时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题:
(1)请你求出:①在0≤x<2的时间段内,y与x的函数关系式;
②在x≥2时间段内,y与x的函数关系式.
(2)用所求的函数解析式预测完成1620 m的路基工 程,需要挖筑多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com