
【题目】如图1,已知直线y= ![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.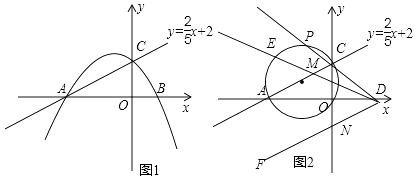
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
【答案】
(1)
解:把x=0代入直线的解析式得:y=2,
∴C(0,2).
把y=0代入直线的解析式得: ![]() x+2=0,解得:x=﹣5,
x+2=0,解得:x=﹣5,
∴A(﹣5,0).
将点A和点C的坐标代入抛物线的解析式得: ![]() ,解得:
,解得: 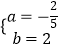 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:令y=0得:﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,解得x=1或x=﹣5,
x+2=0,解得x=1或x=﹣5,
∴B(1,0).
如图1所示:当Q在直线AC上方的抛物线上时.
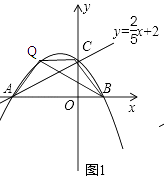
∵△ACQ和△BCQ为同底的三角形,且它们的面积相等,
∴点A和点B到直线CQ的距离相等.
∴QC∥AB.
∵抛物线的对称轴为x=﹣2,
∴点Q与点C关于x=﹣2对称,
∴Q(﹣4,2).
如图2所示:当Q在直线AC下方的抛物线上时.
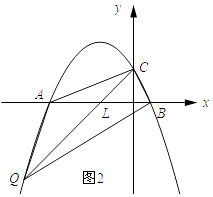
设直线CQ与x轴于点L,则△ACQ的面积= ![]() AL|yC﹣yQ|,△BCQ的面积=
AL|yC﹣yQ|,△BCQ的面积= ![]() BL|yC﹣yQ|.
BL|yC﹣yQ|.
∵△ACQ的面积等于△BCQ的面积,
∴AL=BL.
∴L(﹣2,0).
设直线LC的解析式为y=kx+b,将点C和点L的坐标代入得: ![]() ,解得k=1,b=2.
,解得k=1,b=2.
∴直线CL的解析式为:y=x+2.
将y=x+2与y=﹣ ![]() x2﹣
x2﹣ ![]() x+2联立得:
x+2联立得: 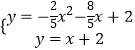 ,解得:
,解得: ![]() 或
或 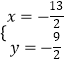 ,
,
∴Q(﹣ ![]() ,﹣
,﹣ ![]() ).
).
综上所述,存在两个符合条件的点:Q(﹣4,2)或Q(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:如图3所示:
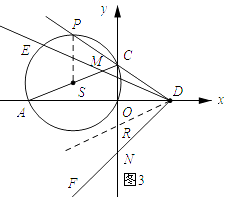
设△AOC的外接圆圆心为S,连接SP,作∠NDR=∠PDE,交y轴于点R,则∠PDR=∠MDN=∠ACO,
∵P是弧ACO的中点,
∴SP平行于y轴,
∴∠PSC=∠ACO=∠CDR,∠SPC=∠RCD,
∴△SCP∽△DCR.
∴△DCR也是等腰三角形,即CD=DR;
又∵DO⊥CR,
∴OC=OR=2.
∴CR=4
∵∠PCS=∠DRC,
∴∠DCM=∠DRN.
在△DCM和△DRN中 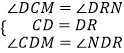 ,
,
∴△DCM≌△DRN.
∴CM=RN.
∴CN﹣CM=CN﹣RN=CR=4
【解析】(1)先求得点A和点C的坐标,然后将点A和点C的坐标代入抛物线的解析式求得a、b的值即可;(2)先求得点B的坐标,当Q在直线AC上方的抛物线上时.△ACQ和△BCQ为同底的三角形,则QC∥AB,依据抛物线的对称性质可求得点Q的坐标;当Q在直线AC下方的抛物线上时.设直线CQ与x轴于点L,由△ACQ的面积等于△BCQ的面积,可知AL=BL,然后求得CL的解析式,最后求得LC与抛物线的交点坐标即可;(3)设△AOC的外接圆圆心为S,连接SP,作∠NDR=∠PDE,交y轴于点R,先证明△SCP∽△DCR,则CD=DR,依据等腰三角形三线合一的性质可知OC=OR=2.然后再证明△DCM≌△DRN,则CM=RN,最后证明CN﹣CM=CR即可.
【考点精析】利用二次函数的概念对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数.


科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点(-3,-2).
的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少? 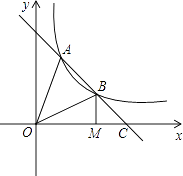
查看答案和解析>>
科目:初中数学 来源: 题型:
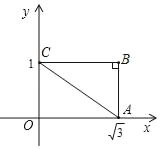
【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(![]() ,0),C(0,1).
,0),C(0,1).
(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
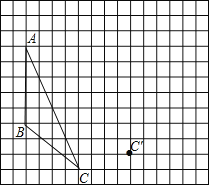
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
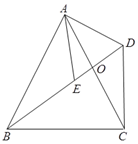
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com