
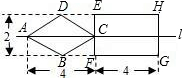
 如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )| A. | 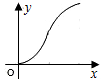 | B. | 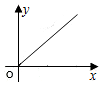 | C. | 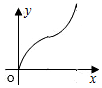 | D. | 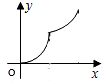 |
分析 先根据Rt△COD中,OD=1,CO=2,求得CD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,再设菱形ABCD沿直线l从左向右匀速运动的速度为v,则CR=vx,分两种情况进行讨论:当EF与CD、CB分别交于M,N时;当EF与AD、AB分别交于P,Q时,分别根据相似三角形的性质,得出菱形进入矩形内部的周长y与运动的时间x之间的函数关系式,即可得出结论.
解答 解:如图,Rt△COD中,OD=1,CO=2,
∴CD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
设菱形ABCD沿直线l从左向右匀速运动的速度为v,则CR=vx,
如图所示,当EF与CD、CB分别交于M,N时,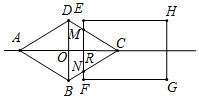
∵MN∥DB,
∴$\frac{CR}{CO}$=$\frac{CM}{CD}$,即$\frac{vx}{2}$=$\frac{CM}{\sqrt{5}}$,
∴CM=$\frac{\sqrt{5}}{2}$vx,
∴y=2CM=$\sqrt{5}$vx,
如图所示,当EF与AD、AB分别交于P,Q时,AR=4-vx,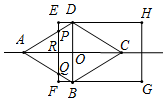
∵PQ∥DB,
∴$\frac{AR}{AO}$=$\frac{AP}{AD}$,即$\frac{4-vx}{2}$=$\frac{AP}{\sqrt{5}}$,
∴AP=$\frac{\sqrt{5}}{2}$(4-vx),
∴PD+DC=2$\sqrt{5}$-$\frac{\sqrt{5}}{2}$(4-vx),
∴y=2(PD+DC)=2[2$\sqrt{5}$-$\frac{\sqrt{5}}{2}$(4-vx)]=$\sqrt{5}$vx,
综上所述,菱形进入矩形内部的周长y与运动的时间x之间的函数关系式为:y=$\sqrt{5}$vx(v为常数,x>0),
故选:B.
点评 本题主要考查了动点问题的函数图象,函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
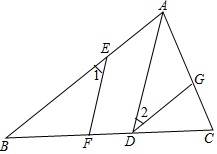 已知:如图,点D、E、G分别是△ABC边BC、AB和AC上的点,AD∥EF,点F在BC上,∠1=∠2=∠B.
已知:如图,点D、E、G分别是△ABC边BC、AB和AC上的点,AD∥EF,点F在BC上,∠1=∠2=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
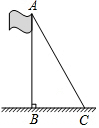 如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.
如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com