
【题目】如图:三角形ABC内接于圆O,∠BAC与∠ABC的角平分线AE,BE相交于点E,延长AE交外接圆O于点D,连接BD,DC,且∠BCA=60°
(1)求∠BED的大小;
(2)证明:△BED为等边三角形;
(3)若∠ADC=30°,圆O的半径为r,求等边三角形BED的边长.
【答案】
(1)解:∵∠BCA=60°,
∴∠BAC+∠ABC=180°-∠BCA=180°-60°=120°,
∵∠BAC与∠ABC的角平分线AE,BE相交于点E,
∴∠ABE+∠BAE= ![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)= ![]() ×120°=60°,
×120°=60°,
∴∠BED=∠ABE+∠BAE=60°
(2)证明:∵∠BCA=60°,
∴∠ADB=∠BCA=60°,
∴∠DBE=180°-∠BED-∠ADB=180°-60°-60°=60°,
∴△BED为等边三角形
(3)解:∵∠ADC=30°,∠ADB=60°,
∴∠BDC=∠ADC+∠ADB=30°+60°=90°,
∴BC是⊙O的直径,
∵∠BCA=60°,
∴∠ABC=90°-60°=30°,
∵BE平分∠ABC,
∴∠CBE=15°,
∴∠DBC=∠DBE-∠CBE=60°-15°=45°,
∴BD=BCcos45°=2r× ![]() =
= ![]() r.
r.
即等边△BED的边长为 ![]() r
r
【解析】(1)根据三角形内角和定理和三角形的一个外角等于和它不相邻的两个内角的和,求出∠BED的值;(2)根据圆周角定理和三角形内角和定理得到△BED为等边三角形;(3)根据圆周角定理,得到BC是⊙O的直径,根据角平分线定义求出∠CBE的度数,根据三角函数求出等边△BED的边长.
【考点精析】掌握圆周角定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】A、B两地相距3000米,甲、乙两人沿同一条路从A地到B地,l1,l2分别表示甲乙两人离开A地的距离y(m)与时间x(min)之间的关系,根据图象填空:
(1)甲出发 min后,乙才出发;
(2) 先到达终点
(3)乙的速度是 m/min.
(4)乙出发后 min追上甲,这时他们距离B地 m

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某治安巡警分队常常在一条东西走向的街道上巡逻一天 下午,该巡警分队驾驶电动小汽车从位于这条街道上的某岗亭出发巡逻,如果规定向东为正,向西为负,他们行驶里程(单位: km)如下:![]() 问:
问:
(1)这辆小汽车完成巡逻后位于该岗亭的那一侧?距离岗亭有多少千米?
(2)已知这种电动小汽车平均每千米耗电![]() 度,则这天下午小汽车共耗电多少度?
度,则这天下午小汽车共耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校餐厅计划购买12张餐桌和若干把餐椅,先从甲、乙两个商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为60元,甲商场规定:购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八折销售.
(1)若学校计划购买12张餐桌和12把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为
(2)若学校计划购买![]()
![]() 把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为 ;
把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为 ;
(3)若学校计划购进20张餐桌和40把餐椅,请通过计算说明,到哪个商场购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
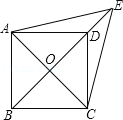
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.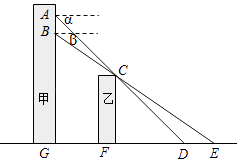
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)
(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题. 
(1)样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com