
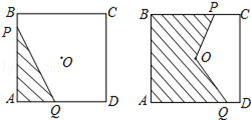
 如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )| A. | 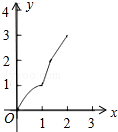 | B. | 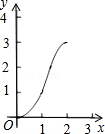 | C. | 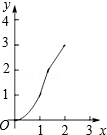 | D. | 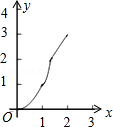 |
分析 过点O作OE⊥CD,根据正方形的性质可得OE=1cm,然后根据梯形的中位线等于两底和的一半求出橡皮筋经过点O的时间为$\frac{4}{3}$,再分①0≤t≤1时,扫过的面积y=S△APQ;②1<t≤$\frac{4}{3}$时,表示出BP,再根据扫过的面积y=S梯形ABPQ;③$\frac{4}{3}$<t≤2时,扫过的面积y=S正方形ABCD-S梯形POEC-S梯形OQDE列式整理即可得解.
解答 解:如图,过点O作OE⊥CD,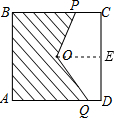 ∵正方形的边长为2cm,点O是对称中心,
∵正方形的边长为2cm,点O是对称中心,
∴OE=$\frac{1}{2}$×2=1cm,
橡皮筋经过点O时,$\frac{2t-2+t}{2}$=1,
解得t=$\frac{4}{3}$,
①0≤t≤1时,扫过的面积y=S△APQ=$\frac{1}{2}$•t•2t=t2
②1<t≤$\frac{4}{3}$时,BP=2t-2,
扫过的面积y=S梯形ABPQ=$\frac{1}{2}$(2t-2+t)×2=3t-2;
③$\frac{4}{3}$<t≤2时,扫过的面积y=S正方形ABCD-S梯形POEC-S梯形OQDE,
=22-$\frac{1}{2}$(4-2t+1)×1-$\frac{1}{2}$(2-t+1)×1,
=4-$\frac{5}{2}$+t-$\frac{3}{2}$+$\frac{1}{2}$t,
=$\frac{3}{2}$t;
纵观各选项,只有C选项图象符合.
故选:C.
点评 本题考查了动点问题函数图象,利用点运动的几何性质列出有关的函数关系式,然后根据函数关系式判断函数图象,注意自变量的取值范围.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:判断题
由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为80000元,今年销售额只有60000元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于18400元且不少于17600万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金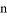 元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,
元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同, 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
计算(-a)3·(a2)3·(-a)2的结果正确的是( )
A. -a11 B. a11 C. -a10 D. a13
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
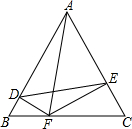 △ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,
△ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
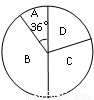
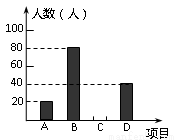
(1)这次被调查的学生共有 人,在扇形统计图中“D”对应的圆心角的度数为 ;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 荷花小区要在一块一边靠墙(墙长是15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,如图所示.若设花园BC的边长为xm,花园的面积为y m2.
荷花小区要在一块一边靠墙(墙长是15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,如图所示.若设花园BC的边长为xm,花园的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
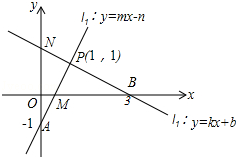 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com