
【题目】在△ABC中,∠A![]() 90°,AB
90°,AB![]() AC.
AC.
(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“![]() ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);
(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB![]()
![]() PA.
PA.
①如图2,点P在△ABC内,∠ABP![]() 30°,求∠PAB的大小;
30°,求∠PAB的大小;
②如图3,点P在△ABC外,连接PC,设∠APC![]() α,∠BPC
α,∠BPC![]() β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.

【答案】(1)否;(2)①45°;②![]() .
.
【解析】试题分析:
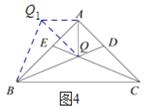
(1)如图4,把△AQC顺时针旋转90°得到△AQ1B,连接QQ1,则由题意易得QQ1=![]() AQ,由已知条件可证∠BQ1Q
AQ,由已知条件可证∠BQ1Q![]() ∠Q1BQ,从而可得BQ
∠Q1BQ,从而可得BQ![]() QQ1=
QQ1=![]() AQ;
AQ;
(2)①如图5,过点PD⊥AB于点,结合∠ABP=30°可得PD=![]() PB,结合PB=
PB,结合PB=![]() PA可得PD=
PA可得PD=![]() PA,由此即可得到sin∠PAB=
PA,由此即可得到sin∠PAB=![]() ,结合∠PAB是锐角即可得到∠PAB=45°;
,结合∠PAB是锐角即可得到∠PAB=45°;
②如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,由此可得PD=![]() PA,结合PB=
PA,结合PB=![]() PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2=
PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2= ![]() ,可得∠1+∠3=90°-
,可得∠1+∠3=90°- ![]() =∠ADP=45°,变形即可得到:
=∠ADP=45°,变形即可得到: ![]() .
.
试题解析:
(1)如图4,把△AQC绕点A顺时针旋转90°得到△AQ1B,连接QQ1,
由旋转的性质可得:AQ1=AQ,∠Q1AQ=90°,
∴QQ1=![]() AQ,
AQ,
∵BQ、CQ分别平分∠ABC、∠ACB,
∴AQ平分∠BAC,
∴∠AQ1C=∠AQC=112.5°,
∴∠BQ1Q=112.5°-45°=67.5°,
∵∠Q1BQ=45°,
∴∠Q1BQ![]() ∠BQ1Q,
∠BQ1Q,
∴BQ![]() Q1Q=
Q1Q=![]() AQ.
AQ.
故答案为:“否”;
(2)① 如图5,作PD⊥AB于D,则∠PDB=∠PDA=90°,

∵ ∠ABP=30°,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵∠PAB是锐角,
∴∠PAB=45°.
②![]() ,理由如下:
,理由如下:
如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,
∴![]() ,∠ADP=∠APD=45°.
,∠ADP=∠APD=45°.
又∵![]() ,
,
∴ PD=PB=CD.
∴ ∠DCP=∠DPC.
∵ ∠APC![]() α,∠BPC
α,∠BPC![]() β,
β,
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】无人机技术我国逐渐发展迅速,全球首款吨位级货运无人机从设计到总装在四川成都双流区完成,现有两架航拍无人机:1号无人机从海拔5米处出发,以1米/秒的速度上升。与此同时,2号无人机从海拔15米处出发,以0.5米/秒的速度上升(设无人机上升时间为![]() 秒)。
秒)。
(1)求出1号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式和2号无人机所在位置的海拔
之间的关系式和2号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式?
之间的关系式?
(2)在某一时刻两架无人机能否位于同一高度?如果能,请求出无人机上升的时间与高度?如果不能,请说明理由.
(3)上升多少时间,两架无人机所在位置的海拔相差5米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前2个小时为生产磨合期,2个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式,他们每人生产的零件总数![]() (个)与生产时间
(个)与生产时间![]() (小时)的关系如图所示,根据图象回答:
(小时)的关系如图所示,根据图象回答:
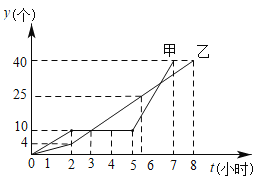
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时?
(2)当![]() 为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
(3)设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1
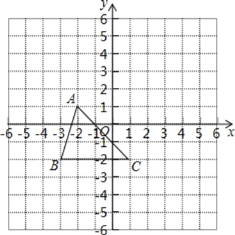
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若直线BC上有一点P,使△PAC的面积是△ABC面积的2倍,直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围
解:∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1.∴y>﹣1.
又∵y<0,∴﹣1<y<0. …①
同理得:1<x<2. …②
由①+②得﹣1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
已知关于x、y的方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)已知a﹣b=3,且b≤1,求a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
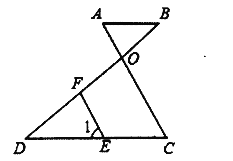
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若|a|=-b,|b|=b,则a=b=0;②若-a不是正数,则a为非负数;③|-a![]() |=(-a)
|=(-a)![]() ; ④若
; ④若![]() ,则
,则![]() ; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com