
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.

(1)求证:AB=BN;
(2)若MD=4,CD=2.4,求![]() 。
。
(3)若AM=2,CN=1.2,求⊙O的半径长。
【答案】(1)见解析;(2)![]() ;(3)3
;(3)3
【解析】
(1)连接OD,由MD切⊙O于点D,得到OD⊥MD,由于BN⊥MC,得到OD∥BN,得出∠ADO=∠N,根据等腰三角形的性质和等量代换可得结果;(2)利用题目条件证明△ADH≌△NDC,从而得到DH=DC=2.4,MH=4-2.4=1.6,MC=4+2.4=6.4,然后利用平行线分线段成比例定理求得![]() 的值;(3)设圆的半径为x,由题目条件证得OD∥AH,然后得到△MAH∽△MOD,根据相似三角形的性质列出比例式求解.
的值;(3)设圆的半径为x,由题目条件证得OD∥AH,然后得到△MAH∽△MOD,根据相似三角形的性质列出比例式求解.
解:(1)连接OD

∵MD切⊙O于点D
∴OD⊥MD
又∵BN⊥MD于点C
∴OD∥BN
∴∠ADO=∠N
又∵OD=OA
∴∠OAD=∠ADO
∴∠OAD=∠N
∴AB=BN;
(2)过点A作AH⊥MC

∵OD∥BN
∴![]()
∴OD=DN
又∵AH⊥MC,BN⊥MD
∴AH∥BN
∴∠HAD=∠N
又∵∠ADH=∠NDC
∴△ADH≌△NDC
∴DH=DC=2.4,MH=4-2.4=1.6,MC=4+2.4=6.4
∴![]()
(3)设⊙O的半径为x,
∵MD切⊙O于点D
∴OD⊥MD
又∵AH⊥MC,
∴OD∥AH
∴△MAH∽△MOD
∴![]()
又∵△ADH≌△NDC
∴AH=CN=1.2
∴![]()
得x=3,
经检验x=3是原分式方程的解
即⊙O的半径为3


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
理清思路,本题证明的思路可用下列框图表示:

根据上述思路,请你完成下列问题.
(1)若BP平分∠ABO,其余条件不变.求证:AP=CD.
(2)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系,并证明得出的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点,过点P作平行于y轴的直线PM,交线段BC于M,当△PCM是以PM为腰的等腰三角形时,点P的坐标是( )

A.(2,-3)或(![]() +1,—2)B.(2,-3)或(
+1,—2)B.(2,-3)或(![]() ,-1-2
,-1-2![]() )
)
C.(2,-3)或(![]() ,-1-2
,-1-2![]() )D.(2,-3)或(3-
)D.(2,-3)或(3-![]() ,2-4
,2-4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCO的边OC在x轴的正半轴上,边OA在y轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限的图象经过其对角线OB的中点D,交边BC于点E,过点E作EG∥OB交x轴于点F,交y轴于点G、若点B的坐标是(8,6),则四边形OBEG的周长是_____.
(k≠0)在第一象限的图象经过其对角线OB的中点D,交边BC于点E,过点E作EG∥OB交x轴于点F,交y轴于点G、若点B的坐标是(8,6),则四边形OBEG的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.
(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45度时,若AD=DE=2,AB=6,求此时线段CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,需添加一个条件,则以下所添加的条件不正确的是( )

A.∠ABD=∠CB.∠ADB=∠ABCC.![]() =
=![]() D.
D.![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )
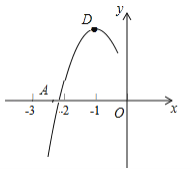
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com