
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬������
Ϊ����ԭ�㣬������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ����
����![]() �ڵڶ������������ϣ�����
�ڵڶ������������ϣ�����![]() ���߶�
���߶�![]() ���߶�
���߶�![]() �ڵ�
�ڵ�![]() ��
��
��1���������ߵı���ʽ��
��2����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��3����֪��![]() ���������߶Գ���ĶԳƵ�Ϊ��
���������߶Գ���ĶԳƵ�Ϊ��![]() ������
������![]() ����
����![]() ��
��![]() ���ϣ���
���ϣ���![]() ʱ��
ʱ��
�����������������е�![]() �����ꣻ
�����ꣻ
�ڵ���![]() ���߶�
���߶�![]() ��ʱ����
��ʱ����![]() ���߶�
���߶�![]() ��һ�㣬
��һ�㣬![]() ������
������![]() �����߶�
�����߶�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ������
������![]() ��ֱ��д���߶�
��ֱ��д���߶�![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3����
����3����![]() ��
��![]() ����
����![]()
��������
��1������A��B����������ʽ��ɣ�
��2���������C��������0,3��������C��CG��OP��G������![]() ��
��![]() ��
��![]() �õ�
�õ�![]() ������P��PF��x����F������E��EN��PF��N���õ�
������P��PF��x����F������E��EN��PF��N���õ�![]() �����P������Ϊ��a��
�����P������Ϊ��a��![]() �������ֱ��BC�Ľ���ʽΪy=x+3���õ�E��
�������ֱ��BC�Ľ���ʽΪy=x+3���õ�E��![]() ��
��![]() +3��������2PF=5PN�õ�5(
+3��������2PF=5PN�õ�5(![]() -
-![]() -3)=2(
-3)=2(![]() )�����xֵ���ɵõ���P�����ꣻ
)�����xֵ���ɵõ���P�����ꣻ
��3��������������ߵĶԳ�����ֱ��x=-1���õ�N��-2,3�������ֱ��BN�Ľ���ʽΪy=3x+9�����������������H��OB֮��ʱ����![]() ���õ�BN��CH���õ�ֱ��CH�Ľ���ʽΪy=3x+3�����������H������Ϊ��-1,0��������H�ڵ�B���ʱ��CH��BN��M����ֱ��OM����
���õ�BN��CH���õ�ֱ��CH�Ľ���ʽΪy=3x+3�����������H������Ϊ��-1,0��������H�ڵ�B���ʱ��CH��BN��M����ֱ��OM����![]() �õ�BM=MC����OM��BC�Ĵ�ֱƽ���ߣ��������M������Ϊ��-
�õ�BM=MC����OM��BC�Ĵ�ֱƽ���ߣ��������M������Ϊ��-![]() ��
��![]() ���������ֱ��CM�Ľ���ʽΪy=
���������ֱ��CM�Ľ���ʽΪy=![]() x+3�����ɵõ���H������Ϊ��-9,0��������ͼ1������Q��x���·���MH��x��ʱ��MH��С����QG��x�ᣬ����M��MF��QG��F�����ı���MHGF�Ǿ��Σ�֤����BQG�ա�QMF���õ�FM=GQ��BG=FQ�����ù��ɶ������GQ=GH=
x+3�����ɵõ���H������Ϊ��-9,0��������ͼ1������Q��x���·���MH��x��ʱ��MH��С����QG��x�ᣬ����M��MF��QG��F�����ı���MHGF�Ǿ��Σ�֤����BQG�ա�QMF���õ�FM=GQ��BG=FQ�����ù��ɶ������GQ=GH=![]() ���õ�MH=FG=BG-FG=
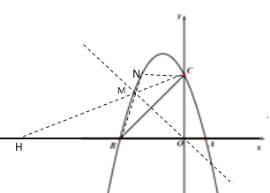
���õ�MH=FG=BG-FG=![]() ����ͼ2������Q��x���Ϸ�����MH��x��ʱ��MH�����Q��QG��x�ᣬQF��MH��F�����ı���HGQF�Ǿ��Σ�ͬ������BGQ�ա�MFQ���õ�QG=FQ=HG��BG=MF�����ù��ɶ������GQ=GH=
����ͼ2������Q��x���Ϸ�����MH��x��ʱ��MH�����Q��QG��x�ᣬQF��MH��F�����ı���HGQF�Ǿ��Σ�ͬ������BGQ�ա�MFQ���õ�QG=FQ=HG��BG=MF�����ù��ɶ������GQ=GH=![]() ���õ�MH=BG+FH=
���õ�MH=BG+FH=![]() �����ɵõ�MH��ȡֵ��Χ.
�����ɵõ�MH��ȡֵ��Χ.
��1������A��B���������![]() ����
����
![]() �����
�����![]() ��
��
�������ߵı���ʽΪ![]() ��
��
��2����x=0ʱ��y=3�����C������Ϊ��0,3����
����C��CG��OP��G��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����P��PF��x����F������E��EN��PF��N��
��EN��OF��
��![]() ,
,
���P��������a��![]() ����
����
��OF=-a��EN=-![]() ��
��
���E�ĺ�����Ϊ![]() ��
��
��B��3,0����C��0,3����
��ֱ��BC�Ľ���ʽΪy=x+3��
��x=![]() ʱ��y=
ʱ��y=![]() +3��
+3��
��E��![]() ��
��![]() +3����
+3����
��2PF=5PN��
��5(![]() -
-![]() -3)=2(
-3)=2(![]() ),
),
���![]() ��
��![]() ��
��
���P��������-1,4����-2,3����
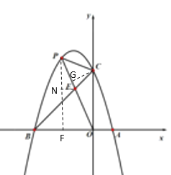
��3���١�![]()
![]() ��
��
�������ߵĶԳ�����ֱ��x=-1��
�ߵ�![]() ���������߶Գ���ĶԳƵ�Ϊ��
���������߶Գ���ĶԳƵ�Ϊ��![]() ��C��0,3����
��C��0,3����
��N��-2,3����
��ֱ��BN�Ľ���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��BN�Ľ���ʽΪy=3x+9��
����H��OB֮��ʱ����ͼ��
��![]() ��
��
��BN��CH��
��ֱ��CH�Ľ���ʽΪy=3x+m������C��������룬��m=3,
��ֱ��CH�Ľ���ʽΪy=3x+3��
��y=0ʱ����x=-1��
���H��������-1,0����
����H�ڵ�B���ʱ����ͼ��CH��BN��M����ֱ��OM��
��![]() ��
��
��BM=MC��
��OB=OC��
��OM��BC�Ĵ�ֱƽ���ߣ�
��ֱ��OM�Ľ���ʽΪy=-x��
�ⷽ����![]() ����
����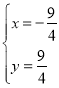 ��
��
���M��������-![]() ��
��![]() ����
����
��ֱ��CM�Ľ���ʽΪy=cx+n��
��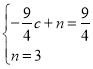 ����
����![]() ��
��
��ֱ��CM�Ľ���ʽΪy=![]() x+3��
x+3��
��y=0ʱx=-9�����H������Ϊ��-9,0����
���ϣ���![]() ʱ����H������Ϊ��-1,0����-9��0����
ʱ����H������Ϊ��-1,0����-9��0����
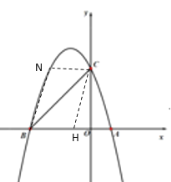
����ͼ1������Q��x���·���MH��x��ʱ��MH��С����QG��x�ᣬ����M��MF��QG��F�����ı���MHGF�Ǿ��Σ�
��FM=GH��FG=MH��
�ߡ�BQM=��F=90����
���BQG+��FQM=��FMQ+��FQM=90����
���BQG=��FMQ��
�ߡ�BGQ=��F��BQ=MQ��
���BQG�ա�QMF��
��FM=GQ��BG=FQ��
��GQ=FM=GH��
��QH=1��
��GQ=GH=![]() ��
��
�� MH=FG=BG-FG=![]() ��
��
��ͼ2������Q��x���Ϸ�����MH��x��ʱ��MH�����Q��QG��x�ᣬQF��MH��F�����ı���HGQF�Ǿ��Σ�
��FQ=HG��FH=QG��
ͬ������BGQ�ա�MFQ��
��QG=FQ=HG��BG=MF��
��QH=1��
��GQ=GH=![]() ��
��
��MH=BG+FH=![]() ��
��
��MH��ȡֵ��Χ��![]() .
.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
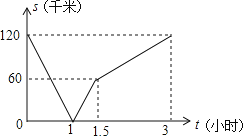
����Ŀ������Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ��ǧ�ף�������ʻ ��ʱ��Ϊt����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��ٳ���1Сʱʱ���ס�����;���������ڳ���1.2Сʱʱ���ұȼ���ʻ��50ǧ�ף����ҵ��յ�ʱ�������յ㻹��60ǧ�ף��ܼ��ٶ������ٶȵ�һ�룮���У���ȷ������ _____________ ��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
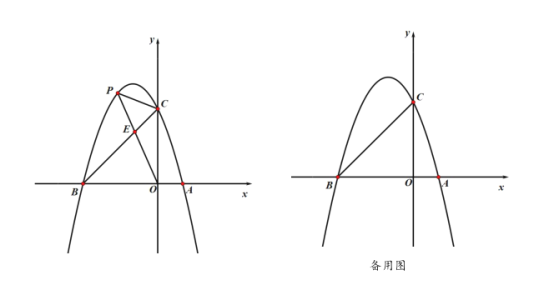
����Ŀ����ͼ��������y=ax2+bx+2��x����A����1��0����B��4��0�����㣬��y���ڵ�C�������C��ƽ����x���ֱ�߽�����һ��D����P����������һ���㣮
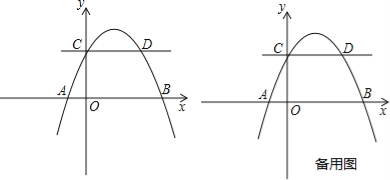
��1���������߽���ʽ����D���ꣻ
��2����E��x���ϣ�����A��E��D��PΪ������ı�����ƽ���ı��Σ����ʱ��P�����ꣻ
��3������P��ֱ��CD�Ĵ��ߣ�����ΪQ��������CPQ��CP���ۣ���Q�Ķ�Ӧ��ΪQ�����Ƿ���ڵ�P��ʹQ��ǡ������x���ϣ������ڣ������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʵ�����е�һ�ְڶ�װ�ã�BC�ڵ����ϣ�֧��ABC�ǵױ�ΪBC�ĵ���ֱ�������Σ��ڶ���AD���Ƶ�A��ת���ڶ���DM���Ƶ�D��ת��AD��30��DM��10��

��1������ת�����У�
�ٵ�A��D��M������ͬһֱ����ʱ����AM�ij���
�ڵ�A��D��M����Ϊͬһֱ�������εĶ���ʱ����AM�ij���
��2�����ڶ���AD˳ʱ����ת90������D��λ������ABC��ĵ�D1ת�����ڵĵ�D2��������D1D2����ͼ2����ʱ��AD2C��135����CD2��60����BD2�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��12���ǵ�41��ֲ���ڣ�ij��λ������չֲ�������������ס����������磬��800Ԫ�����������Ŀ�������680Ԫ������������Ŀ�����ͬ����������ÿ�ñȼ�������ÿ����6Ԫ��
��1�����������ÿ�ö���Ԫ��
��2��������3800Ԫ����ס����������繲100�ã�������Ҫ��������������ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���С˧��ͬѧ�ֱ�Ӽس����������г���ͬһ��·���ҵزμ����ʵ�������ͼ����![]() ���߶�
���߶�![]() �ֱ��ʾС���С˧��صľ���
�ֱ��ʾС���С˧��صľ���![]() ����λ��ǧ�ף���ʱ��
����λ��ǧ�ף���ʱ��![]() ����λ��Сʱ��֮�亯����ϵ��ͼ����С˧�����ҵ�ʱ��С����ҵصľ���Ϊ_________ǧ�ף�
����λ��Сʱ��֮�亯����ϵ��ͼ����С˧�����ҵ�ʱ��С����ҵصľ���Ϊ_________ǧ�ף�
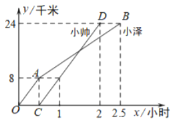
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �IJ���ͼ����ͼ��ʾ����x���һ����������Ϊ
�IJ���ͼ����ͼ��ʾ����x���һ����������Ϊ![]() �������ߵĶԳ�����
�������ߵĶԳ�����![]() ���н����У�
�������
![]() ��
��![]() ��
��![]() ����
����![]() ����������ȵ�ʵ������
����������ȵ�ʵ������![]() ��������x�����һ����������Ϊ
��������x�����һ����������Ϊ![]() ��
��![]() ����
����![]() �ڸ��������ϣ���
�ڸ��������ϣ���![]() ��
��
������ȷ����![]() ����
����![]()

A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���̴������г���8000Ԫ�����˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ���ӣ�ҵĽ��۱�Сӣ�ҵĽ���ÿǧ�˶�20Ԫ.��ӣ���ۼ�Ϊÿǧ��40Ԫ��Сӣ���ۼ�Ϊÿǧ��16Ԫ.
(1)��ӣ�Һ�Сӣ�ҵĽ��۷ֱ���ÿǧ�˶���Ԫ?�������ˮ���̹��˶���ԪǮ?
(2)��ˮ���̵ڶ�������8000ԪǮ�������г������˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ����۲��䣬�������������Сӣ�������20%����Сӣ�ҵ��ۼ۲��䣬Ҫ���õڶ�����Ǯ�����ڵ�һ����Ǯ��90%����ӣ�ҵ��ۼ�����ӦΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���![]() �У�
��![]() ����
����![]() ��ƽ���ı���
��ƽ���ı���![]() �ı��ϣ���
�ı��ϣ���![]() ������
������![]() ����
����![]() ��
��![]() �����߶�
�����߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com