
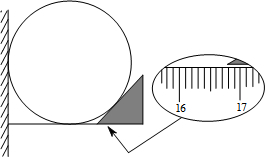
 如图,小明打算用一个45°的三角板和一把带刻度的直尺测量一个圆盘的半径,先将圆盘贴在墙拐角的边沿上,然后将直尺靠在圆盘的下方,直尺的0刻度一端和墙靠在一起,再将45°的三角板的直角边和直尺靠在一起,三角板的斜边和圆盘靠在一起,试通过图中数据求出圆的半径.(精确到0.1)
如图,小明打算用一个45°的三角板和一把带刻度的直尺测量一个圆盘的半径,先将圆盘贴在墙拐角的边沿上,然后将直尺靠在圆盘的下方,直尺的0刻度一端和墙靠在一起,再将45°的三角板的直角边和直尺靠在一起,三角板的斜边和圆盘靠在一起,试通过图中数据求出圆的半径.(精确到0.1) 分析 连接⊙O和各边的切点,设⊙O的半径为r,可得BC=OC=OD=r,由BF=16.8知CF=DF=16.8-r,作DP⊥FH有FP=DFcos∠DFP=$\frac{\sqrt{2}}{2}$(16.8-r)、DE=CP=CF+FP=16.8-r+$\frac{\sqrt{2}}{2}$(16.8-r),作DE⊥OC,根据sin∠DOE=$\frac{DE}{OD}$=$\frac{\sqrt{2}}{2}$列方程求解可得r的值.
解答 解:连接⊙O和各边的切点,即连接OA、OB、OC、OD,
则∠OAB=∠ABC=∠BCO=∠OCP=∠ODF=90°,
∴四边形OABC是矩形,
设⊙O的半径为r,
则BC=OC=OD=r,
由图知BF=16.8,则CF=DF=16.8-r,
过点D作DP⊥FH于点P,
∵∠DFP=45°,
∴FP=DFcos∠DFP=$\frac{\sqrt{2}}{2}$(16.8-r),
∴DE=CP=CF+FP=16.8-r+$\frac{\sqrt{2}}{2}$(16.8-r),
过点D作DE⊥OC于点E,
在Rt△ODE中,∵sin∠DOE=$\frac{DE}{OD}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{16.8-r+\frac{\sqrt{2}}{2}(16.8-r)}{r}$=$\frac{\sqrt{2}}{2}$,
解得:r≈11.9,
答:圆的半径约为11.9cm.
点评 本题主要考查解直角三角形的应用及圆的切线的性质、矩形的判定与性质,熟练掌握圆的切线的性质及三角函数的应用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.
在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C、D两点将线段AB从左到右依次分成2:3:4三部分,点E、F、G分别是AC、CD、DB的中点,且EG=12cm,则AF=7cm.
如图,C、D两点将线段AB从左到右依次分成2:3:4三部分,点E、F、G分别是AC、CD、DB的中点,且EG=12cm,则AF=7cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 “爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2.
“爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com